
【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=![]() ∠A.
∠A.
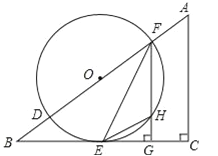
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
【答案】(1)证明过程见解析;(2)![]()
【解析】
试题分析:(1)首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE=![]() ∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)由在△OBE中,sinB=
∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)由在△OBE中,sinB=![]() ,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
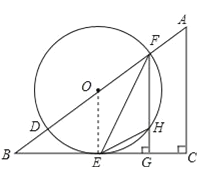
试题解析:(1)连接OE, ∵在△ABC中,∠C=90°,FG⊥BC, ∴∠BGF=∠C=90°, ∴FG∥AC,
∴∠OFG=∠A, ∴∠OFE=![]() ∠OFG, ∴∠OFE=∠EFG, ∵OE=OF, ∴∠OFE=∠OEF, ∴∠OEF=∠EFG,
∠OFG, ∴∠OFE=∠EFG, ∵OE=OF, ∴∠OFE=∠OEF, ∴∠OEF=∠EFG,
∴OE∥FG, ∴OE⊥BC, ∴BC是⊙O的切线;
(2)∵在Rt△OBE中,sinB=![]() ,⊙O的半径为r, ∴OB=
,⊙O的半径为r, ∴OB=![]() r,BE=
r,BE=![]() r, ∴BF=OB+OF=
r, ∴BF=OB+OF=![]() r,
r,
∴FG=BFsinB=![]() r, ∴BG=
r, ∴BG=![]() =
=![]() r, ∴EG=BG﹣BE=
r, ∴EG=BG﹣BE=![]() r,
r,
∴S△FGE=![]() EGFG=
EGFG=![]() r2,EG:FG=1:2, ∵BC是切线, ∴∠GEH=∠EFG, ∵∠EGH=∠FGE,
r2,EG:FG=1:2, ∵BC是切线, ∴∠GEH=∠EFG, ∵∠EGH=∠FGE,
∴△EGH∽△FGE, ∴![]() =(
=(![]() )=
)=![]() , ∴S△EHG=
, ∴S△EHG=![]() S△FGE=
S△FGE=![]() r2.
r2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】给出下面四个命题,其中真命题的个数有( )
(1)平分弦的直径垂直于这条弦,并且平分这条弦所对的弧;
(2)90°的圆周角所对的弦是直径;
(3)在同圆或等圆中,圆心角的度数是圆周角的度数的两倍;
(4)如下图,顺次连接圆的任意两条直径的端点,所得的四边形一定是矩形.
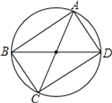
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=160°,OD是∠AOB内任意一条射线,OE平分∠AOD,OC平分∠BOD.
(1)求∠EOC的度数;
(2)若∠BOC=19°,求∠EOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级学生参加冬令营活动,本次冬令营活动分为甲、乙、丙三组进行.如图,条形统计图和扇形统计图反映了学生参加冬令营活动的报名情况,请你根据图中的信息回答下列问题:
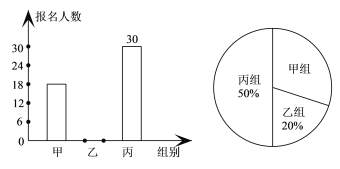
(1)七年级报名参加本次活动的总人数为 ,扇形统计图中,表示甲组部分的扇形的圆心角是 度;
(2)补全条形统计图;
(3)根据实际需要,将从甲组抽调部分学生到丙组,使丙组人数是甲组人数的3倍,则应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋、投放,其中A类指废电池、过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,乙投放的这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)请用画树状图或列表的方法求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,乙团队人数不超过40人.设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.
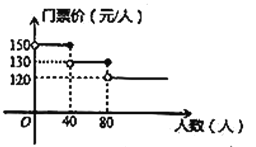
(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变
的函数关系式,并写出自变![]() 的取值范围;
的取值范围;
(2)若甲团队人数不超过80人,计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)端午节之后,该风景区对门票价格作了如下调整:人数不超过40人时,门票价格不变,人数超过40人但不超过80人时,每张门票降价![]() 元;人数超过80人时,每张门票降价
元;人数超过80人时,每张门票降价![]() 元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求
元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
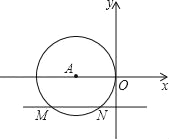
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣8,﹣4),则点N的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
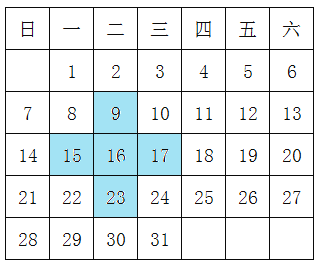
【题目】观察某月的月历,回答下列问题.
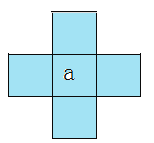
(1)设十字框中间的数为![]() ,求带阴影的十字框中间的5个数的和是多少?
,求带阴影的十字框中间的5个数的和是多少?
(2)小李一家外出游玩了5天,这5天的日期之和是75,小李一家是几号外出的?
(3)在该月的日历上用十字框框出5个数,能使这5个数的和为100吗?如果不能,请说明理由;如果能,请求出十字框中间的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P1是线段AB上一点,AP1=2BP1;点P2是线段P1B上一点,P1P2=2BP2:点P3是线段P2B上一点,P2P3=2BP3 , …请借助所给的图形,计算 ![]() 的结果为________(n为正整数,用含n的代数式表示)
的结果为________(n为正整数,用含n的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com