
分析 将1999×2000×2001×2002转化为[1999×(1999+3)]×[(1999+1)×(1999+2)]=(19992+3×19992)(19992+3×19992+2)=(19992+3×1999)2+2×(19992+3×1999),则1999×2000×2001×2002+1可组成完全平方式(19992+3×1999+1)2,求出其算术平方根即可.
解答 解:∵1999×2000×2001×2002+1,
=[1999×(1999+3)]×[(1999+1)×(1999+2)]+1,
=(19992+3×19992)(19992+3×19992+2)+1,
=(19992+3×1999)2+2×(19992+3×1999)+1,
=(19992+3×1999+1)2,
∴p=$\sqrt{1999×2000×2001×2002+1}$-20022=19992+3×1999+1-20022
=19992+3×1999+1-19992-6×1999-9
=-3×1999-8
=-6005.
故答案为-6005.
点评 本题考查了二次根式的化简计算,解题的关键是将2000×2001×2002×2003首尾相乘,使根号内的式子转化为完全平方式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
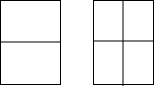 如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么原来矩形的长与宽的比是多少?将这张纸再如上述对折下去,得到的矩形都相似吗?
如图,将一张矩形纸片沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么原来矩形的长与宽的比是多少?将这张纸再如上述对折下去,得到的矩形都相似吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com