
【题目】如图,已知![]() ,
,![]() ,则下列结论: ①
,则下列结论: ①![]() ; ②
; ②![]() ;③点P在
;③点P在![]() 的平分线上,其中正确的是()
的平分线上,其中正确的是()

A.只有①B.只有②C.只有①②D.①②③
【答案】D
【解析】
根据ABAE=ACAD可判断①;证△ABD≌△ACE,推出∠B=∠C,根据AAS证明△BPE≌△CPD即可判断②;连接AP,根据△BPE≌△CPD推出BP=CP,根据SAS证△ABP≌△ACP,推出∠1=∠2即可判断③.
解:∵AB=AC,AD=AE,
∴ABAE=ACAD,
∴EB=DC,①正确;
∵在△ABD和△ACE中,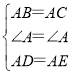 ,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠C,
在△BPE和△CPD中, ,
,
∴△BPE≌△CPD(AAS),②正确;
如图,连接AP,
∵△BPE≌△CPD,
∴BP=CP,
在△ABP和△ACP中, ,
,
∴△ABP≌△ACP(SAS),
∴∠1=∠2,
∴点P在∠BAC的角平分线上,③正确;
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为10的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合).

(Ⅰ)如图1,若点Q是BC边上一动点,与点P同时以相同的速度由C向B运动(与C、B不重合).求证:BP=AQ;
(Ⅱ)如图2,若Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠式可调节的鱼竿支架的示意图,AE是地插,用来将支架固定在地面上,支架AB可绕A点前后转动,用来调节AB与地面的夹角,支架CD可绕AB上定点C前后转动,用来调节CD与AB的夹角,支架CD带有伸缩调节长度的伸缩功能,已知BC=60cm.
(1)若支架AB与地面的夹角∠BAF=35°,支架CD与钓鱼竿DB垂直,钓鱼竿DB与地面AF平行,则支架CD的长度为 cm(精确到0.1cm);(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70).
(2)如图2,保持(1)中支架AB与地面的夹角不变,调节支架CD与AB的夹角,使得∠DCB=85°,若要使钓鱼竿DB与地面AF仍然保持平行,则支架CD的长度应该调节为多少?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用配方法求出抛物线![]() 的顶点坐标、对称轴、最大值或最小值;若将抛物线
的顶点坐标、对称轴、最大值或最小值;若将抛物线![]() 先向左平移
先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,所得抛物线的函数关系式为________.
个单位,所得抛物线的函数关系式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与两坐标轴分别交于
的图象与两坐标轴分别交于![]() ,
,![]() ,
,![]() 三点,一次函数的图象与抛物线交于
三点,一次函数的图象与抛物线交于![]() ,
,![]() 两点.
两点.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 当两函数的函数值都随着
当两函数的函数值都随着![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
![]() 当自变量
当自变量![]() 满足什么范围时,一次函数值大于二次函数值.
满足什么范围时,一次函数值大于二次函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i为1∶![]() ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
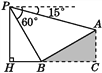
A. 15米 B. 20![]() 米 C. 20
米 C. 20![]() 米 D. 10
米 D. 10![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列各题:
(1)先化简,再求代数式(![]() 的值,其中x=
的值,其中x=![]() cos30°+
cos30°+![]() ;
;
(2)已知α是锐角,且sin(α+15°)=![]() .计算
.计算![]() -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+(![]() )-1的值.
)-1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD,BD,DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,以AC为斜边向外作等腰直角三角形COA,已知BC=8,OB=10![]() ,则另一直角边AB的长为__________.
,则另一直角边AB的长为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com