
【题目】如图,![]() 中,点
中,点![]() 是边
是边![]() 上一个动点,过
上一个动点,过![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的平分线于点
的平分线于点![]() .
.

![]() 探究:线段
探究:线段![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
![]() 当点
当点![]() 运动到何处时,且
运动到何处时,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?
是正方形?
![]() 当点
当点![]() 在边
在边![]() 上运动时,四边形
上运动时,四边形![]() ________是菱形吗?(填“可能”或“不可能”)
________是菱形吗?(填“可能”或“不可能”)
【答案】(1)OE=OF;(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形;(3)不可能.
【解析】
(1)由直线MN∥BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,易证得△OEC与△OFC是等腰三角形,则可证得OE=OF=OC;
(2)正方形的判定问题,AECF若是正方形,则必有对角线OA=OC,所以O为AC的中点,同样在△ABC中,当∠ACB=90°时,可满足其为正方形;
(3)菱形的判定问题,若是菱形,则必有四条边相等,对角线互相垂直.
(1)OE=OF.理由如下:
∵CE是∠ACB的角平分线,∴∠ACE=∠BCE.
又∵MN∥BC,∴∠NEC=∠ECB,∴∠NEC=∠ACE,∴OE=OC.
∵OF是∠BCA的外角平分线,∴∠OCF=∠FCD.
又∵MN∥BC,∴∠OFC=∠ECD,∴∠OFC=∠COF,∴OF=OC,∴OE=OF;
(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由如下:
∵当点O运动到AC的中点时,AO=CO.
又∵EO=FO,∴四边形AECF是平行四边形.
∵FO=CO,∴AO=CO=EO=FO,∴AO+CO=EO+FO,即AC=EF,∴四边形AECF是矩形.
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,∴AC⊥EF,∴四边形AECF是正方形;
(3)不可能.理由如下:
如图,连接BF.
∵CE平分∠ACB,CF平分∠ACD,∴∠ECF=![]() ∠ACB+
∠ACB+![]() ∠ACD=
∠ACD=![]() (∠ACB+∠ACD)=90°,若四边形BCFE是菱形,则BF⊥EC,但在△GFC中,不可能存在两个角为90°,所以四边形BCFE不能是菱形.
(∠ACB+∠ACD)=90°,若四边形BCFE是菱形,则BF⊥EC,但在△GFC中,不可能存在两个角为90°,所以四边形BCFE不能是菱形.
故答案为:不可能.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)若∠APC=3∠BPC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图l、图2和图3所示(阴影部分为草坪).

请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图l,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(x,0),B(0,y),且x,y满足![]() ,且点A与点C关于y轴对称.
,且点A与点C关于y轴对称.
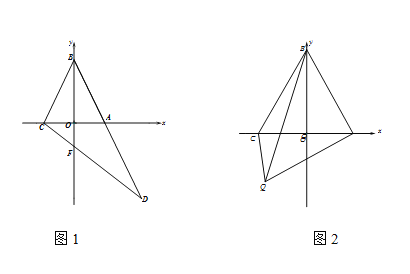
(1)求C坐标;
(2)如图1,点D在射线BA上,连接CD,若b=4,∠D=![]() ∠CBA,求CD长
∠CBA,求CD长
(3)如图2,如图2,BC=2OC,点Q是平面内一点,连接 QB,QC,QA,若QB=m,QC=OA,求AQ最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)
(1)画出格点△ABC关于直线DE的对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点Q,使QA﹣QB最大.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com