
【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=![]() 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.

(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
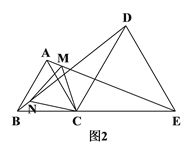
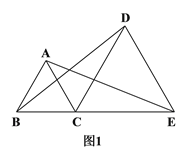
【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com