
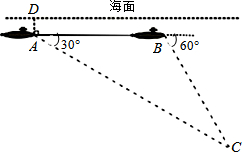
 如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )| A. | 2000米 | B. | 4000米 | C. | 2000$\sqrt{3}$米 | D. | (2000$\sqrt{3}$+500)米 |
分析 由C点向AB作垂线,交AB的延长线于E点,并交海面于F点,易证∠BAC=∠BCA,所以有BA=BC.然后在直角△BCE中,利用正弦函数求出CE的长.
解答 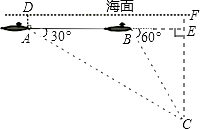 解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
已知AB=4000(米),∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4000(米).
在Rt△BEC中,
EC=BC•sin60°=4000×$\frac{\sqrt{3}}{2}$=2000$\sqrt{3}$(米).
∴CF=CE+EF=2000$\sqrt{3}$+500(米).
故选D.
点评 本题考查了仰俯角问题,解决此类问题的关键是正确的将仰俯角转化为直角三角形的内角并选择正确的边角关系解直角三角形,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:选择题
| A. | 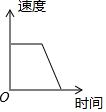 | B. | 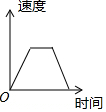 | C. | 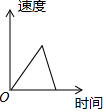 | D. | 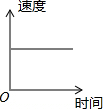 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
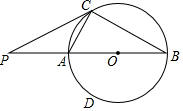 在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.
在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
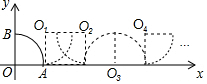 如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )
如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )| A. | (16+4π,0) | B. | (14+4π,2) | C. | (14+3π,2) | D. | (12+3π,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com