
分析 按照有理数的分类填写:有理数$\left\{\begin{array}{l}{整数\left\{\begin{array}{l}{正整数}\\{0}\\{负整数}\end{array}\right.}\\{分数\left\{\begin{array}{l}{正分数}\\{负分数}\end{array}\right.}\end{array}\right.$.
解答 解:(1)正数集合:{+8.5,0.3,12,4$\frac{1}{3}$,…};
(2)整数集合:{0,12,-9,-2,…};
(3)非正整数集合:{0,-9,-2,…};
(4)负分数集合:{-3$\frac{1}{2}$,-3.4,-1.2,…}.
故答案为:8.5,0.3,12,4$\frac{1}{3}$,…;0,12,-9,-2,…;0,-9,-2,…;3$\frac{1}{2}$,-3.4,-1.2,….
点评 本题考查了有理数的分类,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点是解题的关键.注意整数和正数的区别,注意0是整数,但不是正数.


科目:初中数学 来源: 题型:解答题
 已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
已知:如图,PM=PN,∠M=∠N.求证:AM=BN.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,按图中方法将△BCD沿BD折叠,使点C落在边AB上的点C′处,则C′D的长为3.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,按图中方法将△BCD沿BD折叠,使点C落在边AB上的点C′处,则C′D的长为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
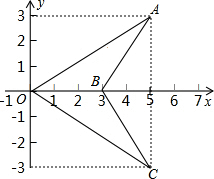 如图,三角形BCO是三角形BAO经过某种变换得到的.
如图,三角形BCO是三角形BAO经过某种变换得到的.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com