
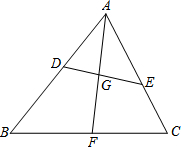
 如图,在△ABC中,D,E分别是AB,AC上的点,∠AED=∠ABC,∠BAC的平分线AF交DE于点G,交BC于点F.
如图,在△ABC中,D,E分别是AB,AC上的点,∠AED=∠ABC,∠BAC的平分线AF交DE于点G,交BC于点F.分析 (1)根据两组对应角相等可判断△ABC∽△AED,△ADG∽△ACF,△AEG∽△ABF.
(2)根据相似三角形的对应高相等可以进行计算.
解答 解:(1)∵∠AED=∠ABC,∠EAD=∠BAC,
∴△ABC∽△AED.
∵∠AED=∠ABC,∠EAG=∠BAF,
∴△AEG∽△ABF.
∵∠EDG=∠ACF,∠DAG=∠CAF,
∴△ADG∽△ACF.
(2)∵$\frac{AG}{GF}$=$\frac{3}{2}$,
∴$\frac{AG}{AF}$=$\frac{3}{5}$,
∵△ADG∽△ACF,
∴$\frac{DE}{BC}$=$\frac{AG}{GF}$=$\frac{3}{5}$.
点评 (1)本题考查了相似三角形的判定,解答本题,要找到两组对应角相等.
(2)本题考查了相似三角形的对应高的比等于相似比,灵活运用是关键.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
| A. | ①②都对 | B. | ①②都错 | C. | ①对②错 | D. | ①错②对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-|{\frac{3}{4}}|$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格中,每个小正方形的边长皆为1.请在网格上画出长度分别为$\sqrt{2}$,$\sqrt{5}$,$\sqrt{17}$的线段.
在如图所示的正方形网格中,每个小正方形的边长皆为1.请在网格上画出长度分别为$\sqrt{2}$,$\sqrt{5}$,$\sqrt{17}$的线段.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com