
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )

A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
【答案】A
【解析】先判断出OA=OB,∠OAB=∠ABO,分两种情况判断出△AOC≌△ABD,进而判断出∠ABD=∠AOB=60°,即可得出结论.
∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴OA=AB,∠OAB=∠ABO=60°
①当点C在线段OB上时,如图1,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD,
在△AOC和△ABD中, ,
,
∴△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠ABE=180°﹣∠ABO﹣∠ABD=60°=∠AOB,
∴BD∥OA;
②当点C在OB的延长线上时,如图2,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD,
在△AOC和△ABD中, ,
,
∴△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠ABE=180°﹣∠ABO﹣∠ABD=60°=∠AOB,
∴BD∥OA,
故选A.




 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,边AB、AC的垂直平分线分别交BC于E、F,若∠EAF=90°,AF=3,AE=4.
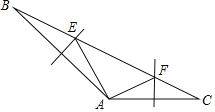
(1)求边BC的长;(2)求出∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在边AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积。
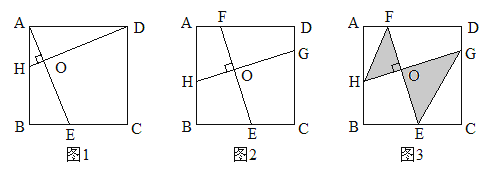
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,BD,CE分别是
中,BD,CE分别是![]() ,
,![]() 平分线,BD,CE相交于点P.
平分线,BD,CE相交于点P.
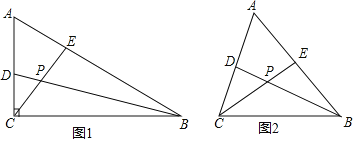
![]() 如图1,如果
如图1,如果![]() ,则
,则![]() ______;
______;
![]() 如图2,如果
如图2,如果![]() ,
,![]() 不是直角,请问在
不是直角,请问在![]() 中所得的结论是否仍然成立?若成立,请证明:若不成立,请说明理由.
中所得的结论是否仍然成立?若成立,请证明:若不成立,请说明理由.
![]() 小月同学在完成
小月同学在完成![]() 之后,发现CD、BE、BC三者之间存在着一定的数量关系,于是她在边CB上截取了
之后,发现CD、BE、BC三者之间存在着一定的数量关系,于是她在边CB上截取了![]() ,连接PF,可证
,连接PF,可证![]() ≌
≌![]() ,请你写出小月同学发现,并完成她的说理过程.
,请你写出小月同学发现,并完成她的说理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有一套火车玩具,有两列火车、一副轨道、一个隧道模型及一个站牌.特别之处:隧道模型也可以像火车一样移动,当火车头进入隧道一瞬间会响起音乐,当火车完全穿过隧道的一瞬间音乐会结束.已知甲火车长![]() 厘米,甲乙两列火车的速度均为
厘米,甲乙两列火车的速度均为![]() 厘米/秒,轨道长
厘米/秒,轨道长![]() 米.
米.
(1)将轨道围成一个圆圈,将甲、乙两列火车紧挨站牌放置,车头方向相反,同时启动,到两车相撞用时![]() 秒,求乙火车的长度?
秒,求乙火车的长度?
(2)在(1)的条件下,乙火车穿过静止的隧道音乐响起了![]() 秒,求隧道的长度;
秒,求隧道的长度;
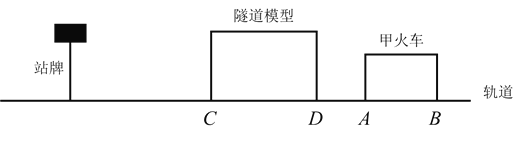
(3)在(1)(2)的条件下,轨道铺成一条直线,把隧道模型、甲火车依次放在站牌的右侧,站牌静止不动,甲火车头与隧道相距![]() (即
(即![]() ).当甲火车向左运动,隧道模型以不变的速度运动,音乐却响了
).当甲火车向左运动,隧道模型以不变的速度运动,音乐却响了![]() 秒;当音乐结束的一瞬间,甲火车头
秒;当音乐结束的一瞬间,甲火车头![]() 与站牌相距乙火车车身的长度,请同学们思考一下,以站牌所在地为原点建立数轴,你能确定甲火车、隧道在运动前的位置吗?如果可以,请画出数轴并标出
与站牌相距乙火车车身的长度,请同学们思考一下,以站牌所在地为原点建立数轴,你能确定甲火车、隧道在运动前的位置吗?如果可以,请画出数轴并标出![]() 运动前的位置.
运动前的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
(1)若从中抽出2张卡片,且这2个数字的差最小,应如何抽取?最小值是多少?
(2)若从中抽出2张卡片,且这2个数字的积最大,应如何抽取?最小值是多少?
(3)若从中抽出4张卡片,运用加、减、乘、除、乘方、括号等运算符号,使得结果为24.请写出运算式.(只需写出一种)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com