
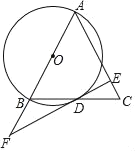
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)已知AB=4,AE=3.求BF的长.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】一种火爆的网红电子产品,每件产品成本![]() 元、工厂将该产品进行网络批发,批发单价
元、工厂将该产品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
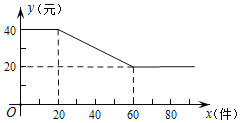
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.
![]() 直接写出
直接写出![]() 与
与![]() 之间所满足的函数关系式,并写出自变量
之间所满足的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 若一次性批发量不超过
若一次性批发量不超过![]() 件,当批发量为多少件时,工厂获利最大?最大利润是多少?
件,当批发量为多少件时,工厂获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
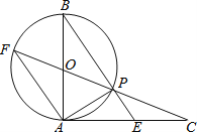
【题目】如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP、AF.
(1)求证:AF∥BE;
(2)求证:![]() ;
;
(3)若AB=2,求tan∠F的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林家的洗手盘台面上有一瓶洗手液(如图1).当手按住顶部A下压如图2位置时,洗手液瞬间从喷口B流出路线呈抛物线经过C与E两点.瓶子上部分是由弧![]() 和弧
和弧![]() 组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,GH=10cm,点E到台面GH的距离为14cm,点B距台面的距离为16cm,且B,D,H三点共线.若手心距DH的水平距离为2cm去接洗手液时,则手心距水平台面的高度为_____cm.
组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,GH=10cm,点E到台面GH的距离为14cm,点B距台面的距离为16cm,且B,D,H三点共线.若手心距DH的水平距离为2cm去接洗手液时,则手心距水平台面的高度为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
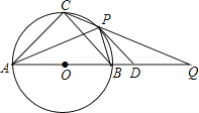
【题目】如图,⊙O为等腰三角形ABC的外接圆,AB是⊙O的直径,AB=12,P为![]() 上任意一点(不与点B,C重合),直线CP交AB的延长线于点Q,⊙O在点P处的切线PD交BQ于点D,则下列结论:①若∠PAB=30°,则
上任意一点(不与点B,C重合),直线CP交AB的延长线于点Q,⊙O在点P处的切线PD交BQ于点D,则下列结论:①若∠PAB=30°,则![]() 的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6
的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6![]() ;④无论点P在
;④无论点P在![]() 上的位置如何变化,CPCQ=108.其中正确结论的序号为 ______.
上的位置如何变化,CPCQ=108.其中正确结论的序号为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
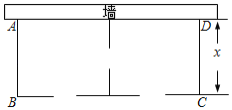
【题目】某农场要建一个饲养场(长方形![]() ,饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长60米,设饲养场(长方形
,饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长60米,设饲养场(长方形![]() 的宽为
的宽为![]() 米.
米.
(1)求饲养场的长![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
(2)若饲养场的面积为![]() ,求
,求![]() 的值.
的值.
(3)当![]() 为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少
为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号)
①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店销售一批水果,平均每天可售出![]() ,每千克盈利
,每千克盈利![]() 元,经调查发现,每千克降价
元,经调查发现,每千克降价![]() 元,商店平均每天可多售出
元,商店平均每天可多售出![]() 水果,则商店平均每天的最高利润为______________ 元
水果,则商店平均每天的最高利润为______________ 元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com