
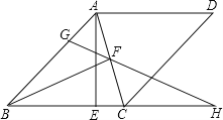
【题目】 菱形ABCD中,F是对角线AC的中点,过点A作AE⊥BC垂足为E,G为线段AB上一点,连接GF并延长交直线BC于点H.
(1)当∠CAE=30°时,且CE=![]() ,求菱形的面积;
,求菱形的面积;
(2)当∠BGF+∠BCF=180°,AE=BE时,求证:BF=(![]() +1)GF.
+1)GF.
【答案】(1)6![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)只要证明△ABC是等边三角形,即可解决问题;
(2)如图,连接GC,作GM⊥GF交BF于M.证明△BGC是等腰直角三角形,再证明△BGM≌△CGF即可解决问题;
(1)∵四边形ABCD是菱形,
∴AB=BC,
∵AE⊥BC,∠EAC=30°,
∴∠ACE=60°,AC=2EC=2![]() ,
,
∴△ABC,△ACD都是等边三角形,
∴S菱形ABCD=2S△ABC=2×![]() ×(2
×(2![]() )2=6
)2=6![]() .
.
(2)如图,连接GC,作GM⊥GF交BF于M.

∵四边形ABCD是菱形,
∴BA=BC,∵AF=FC,
∴BF⊥AC,
∴∠BFA=90°,
∵∠BGF+∠BCF=180°,∠AGF+∠BGF=180°,
∴∠AGF=∠ACB,∵∠GAF=∠CAB
∴△AGF∽△ACB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,∵∠CAG=∠BAF,
,∵∠CAG=∠BAF,
∴△CAG∽△BAF,
∴∠CGA=∠BFA=90°,
∵AE⊥BE,AE=BE,
∴∠ABE=45°,
∴∠GBC=∠GCB=45°,
∴GB=GC,
∵∠BGC=∠MGF,
∴∠BGM=∠CGF,
∵∠GBM=∠GCF,
∴△BGM≌△CGF,
∴BM=CF,GM=GF,FM=![]() GF,
GF,
∵∠AGC=90°AF=FC,
∴GF=FC=BM,
∴BF=BM+FM=GF+![]() GF=(
GF=(![]() +1)GF.
+1)GF.


科目:初中数学 来源: 题型:
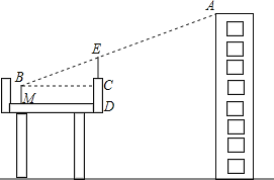
【题目】为了减轻二环高架上汽车的噪音污染,成都市政府计划在高架上的一些路段的护栏上方增加隔音屏.如图,工程人员在高架上的车道M处测得某居民楼顶的仰角∠ABC的度数是20°,仪器BM的高是0.8m,点M到护栏的距离MD的长为11m,求需要安装的隔音屏的顶部到桥面的距离ED的长(结果保留到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
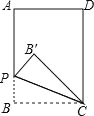
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
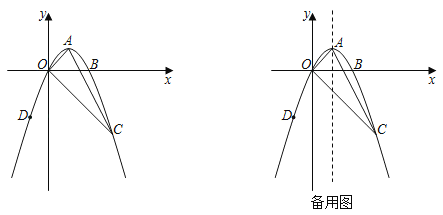
【题目】已知抛物线y=ax2+bx+c与x轴交于O、B两点,其顶点A坐标为(1,1),点C为抛物线在第四象限内的一点,其坐标为(3,﹣3).
(1)求抛物线解析式;
(2)点D为抛物线在第三象限内的一点,过点D向x轴作垂线段,垂足为H,是否存在点D使得△DHO与△AOC相似,如果存在,请求出点D坐标,如果不存在,请说明理由;
(3)点E、F分别为抛物线以及抛物线对称轴上的两动点,请问是否存在以BO为边,B、O、E、F为顶点的平行四边形,如果存在请直接写出点E坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
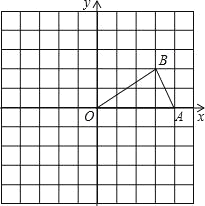
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.
(友情提示:AB=|x2﹣x1|)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小鸣想每天多做几套数学题,妈妈想通过一个游戏决定小鸣多做题的数量:在一个不透鸣的盒子中放入三张卡片,每张卡片上写着一个实数,分别为3,![]() ,2
,2![]() (每张卡片除了上面的实数不同以外其余均相同),妈妈让小鸣从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小鸣每天做五套,否则就多做十套.
(每张卡片除了上面的实数不同以外其余均相同),妈妈让小鸣从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小鸣每天做五套,否则就多做十套.
(1)请你直接写出按照妈妈的规则小鸣每天做五套数学题的概率;
(2)小鸣想和妈妈重新约定游戏规则:自己从盒子中随机抽取两次,每次抽取一张卡片,第一次抽取后记下卡片上的数,再将卡片放回盒中抽取第二次,如果抽取的两数之积是有理数,自己每天做五套数学题,否则每天做十套.用列表法或树状图法求按此规则小鸣每天做十套数学题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:小明用下面的方法求![]() 的解.
的解.
解法 1:令![]() ,则x=t2,原方程化为t -3t2=0,解方程t -3t2=0,得t1=0,t2=
,则x=t2,原方程化为t -3t2=0,解方程t -3t2=0,得t1=0,t2=![]() ,
,
所以![]() 或
或![]() ,将方程
,将方程![]() 或
或![]() 两边平方,得x=0或
两边平方,得x=0或![]() .
.
经检验:x=0或![]() 都是原方程的解,所以原方程的解为x=0或
都是原方程的解,所以原方程的解为x=0或![]() .
.
解法 2:移项,得 ![]() ,方程两边同时平方,得x=9x2,解方程x=9x2,得x=0或
,方程两边同时平方,得x=9x2,解方程x=9x2,得x=0或![]() .
.
经检验:x=0或![]() 都是原方程的解,所以原方程的解为x=0或
都是原方程的解,所以原方程的解为x=0或![]() .
.
(1)定义![]() ,根据定义写出符合条件
,根据定义写出符合条件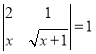 的方程;
的方程;
(2)求出(1)中写出的方程的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com