
 如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=
如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=| 6 |
| 6 |
| AC2-AD2 |
| 2 |
| ||
| 2 |
| x | ||
|
| x | ||
|
| ||
|
| 2 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 26、如图,一副三角饭的两个直角顶点重合在一起,
26、如图,一副三角饭的两个直角顶点重合在一起,查看答案和解析>>
科目:初中数学 来源: 题型:
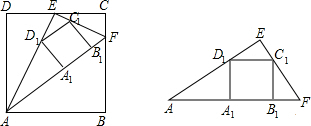
查看答案和解析>>
科目:初中数学 来源: 题型:
学习《图形的相似》后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件.
(1)“对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,两个直角三角形全等” .类似地,你可以等到:“满足 ,或 ,两个直角三角形相似” .
(2)“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地你可以得到“满足 的两个直角三角形相似”。请结合下列所给图形,填出已知中所缺少的条件,并完成说理过程.
已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C![]() =90° .试说明Rt△ABC∽Rt△A’B’C’ .
=90° .试说明Rt△ABC∽Rt△A’B’C’ .

查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《图形的相似》(05)(解析版) 题型:解答题
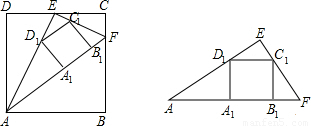
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《四边形》(07)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com