
 随着奥运会成功召开,福娃系列商品也随之热销.一天小林在商场看到一件奥运吉祥物的纪念品,标价为每件33元,他的身边只带有2元和5元两种面值的人民币各若干张,他买了一件这种商品.若无需找零钱,则小林付款方式有哪几种(指付出2元和5元钱的张数)?哪种付款方式付出的张数最少?
随着奥运会成功召开,福娃系列商品也随之热销.一天小林在商场看到一件奥运吉祥物的纪念品,标价为每件33元,他的身边只带有2元和5元两种面值的人民币各若干张,他买了一件这种商品.若无需找零钱,则小林付款方式有哪几种(指付出2元和5元钱的张数)?哪种付款方式付出的张数最少?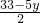

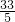 .
.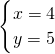 ,
, ,
,
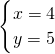 ,得x+y=9
,得x+y=9 得x+y=12
得x+y=12 得x+y=15.
得x+y=15.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
 随着奥运会成功召开,福娃系列商品也随之热销.一天小林在商场看到一件奥运吉祥物的纪念品,标价为每件33元,他的身边只带有2元和5元两种面值的人民币各若干张,他买了一件这种商品.若无需找零钱,则小林付款方式有哪几种(指付出2元和5元钱的张数)?哪种付款方式付出的张数最少?
随着奥运会成功召开,福娃系列商品也随之热销.一天小林在商场看到一件奥运吉祥物的纪念品,标价为每件33元,他的身边只带有2元和5元两种面值的人民币各若干张,他买了一件这种商品.若无需找零钱,则小林付款方式有哪几种(指付出2元和5元钱的张数)?哪种付款方式付出的张数最少?查看答案和解析>>
科目:初中数学 来源:江苏同步题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com