练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

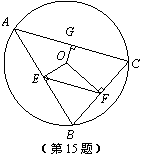
    如图，⊙O的半径是5，△ABC是⊙O的内接三角形，过圆心O分别作AB、BC、AC的垂线，垂足为E、F、G，连接EF． 若OG＝2，则EF为           ．


          

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


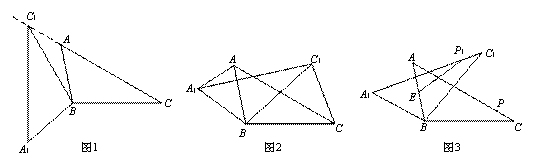
    在△ABC中，AB＝6，BC＝8，∠ACB＝30°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．

    （1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；

    （2）如图2，连接AA1，CC1，若△CBC1的面积为16，求△ABA1的面积；

    （3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转的过程中，点P的对应点是点P1，直接写出线段EP1长度的最大值与最小值．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用半径为6cm的半圆围成一个圆锥的侧面，则圆锥的底面半径等于          cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    利用表格中的数据，可求出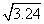＋(4.123)2－   的近似值是(结果保留整数)．

    a

    a2

    17

    289

    4.123

    13.038

    18

    324

    4.243

    13.416

    19

    361

    4.359

    13.784

    A．3

    B．4

    C．5

    D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     (2×103)2×(3×10－3) ＝                 ．（结果用科学计数法表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    甲、乙、丙三位歌手进入“我是歌手”的冠、亚、季军的决赛，他们通过抽签来决定演唱顺序．

    （1）求甲第一位出场的概率；

    （2）求甲比乙先出场的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


         反比例函数y＝ (k为常数,k≠0)的图象是双曲线.当k＞0时，双曲线两个分支分别在

    一、三象限,在每一个象限内,y随x的增大而减小（简称增减性）；反比例函数的图象关于

       原点对称（简称对称性）．   

       这些我们熟悉的性质，可以通过说理得到吗？

      【尝试说理】

    我们首先对反比例函数y＝（k＞0）的增减性来进行说理．

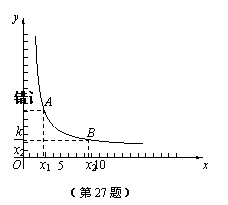
    如图，当x＞0时．

    在函数图象上任意取两点A、B，设A(x1，)，B(x2，)，

    且0＜x1＜ x2．

    下面只需要比较和的大小．

    —＝ ．

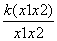    ∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．

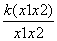    ∴＜0．即＜ ．

    这说明：x1＜ x2时，＞．也就是：自变量值增大了，对应的函数值反而变小了．

    即：当x＞0时，y随x的增大而减小．

    同理，当x＜0时，y随x的增大而减小．

    （1）试说明：反比例函数y＝  （k＞0）的图象关于原点对称．

       【运用推广】

    （2）分别写出二次函数y＝ax2 (a＞0，a为常数)的对称性和增减性，并进行说理．

    对称性：                                             ；

    增减性：                                            ．

    说理：

    （3）对于二次函数y＝ax2＋bx＋c (a＞0，a，b，c为常数)，请你从增减性的角度，简要解释为何当x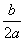＝— 时函数取得最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若，则的值为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


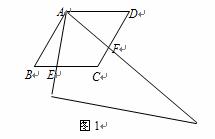
    已知：如图，在菱形ABCD中，∠B= 60°，把一个含60°角的三角尺与这个

    菱形叠合，使三角尺60°角的顶点与点A重合，将三角尺绕点A按逆时针方向旋转 ．

    (1)如图1，当三角尺的两边分别与菱形的两边BC、CD相交于点E、F．

        求证：CE+CF=AB；

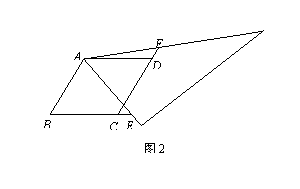
    (2)如图2，当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F．写出此时CE、CF、AB长度之间关系的结论．（不需要证明）

    A
     

     


    查看答案和解析>>

    同步练习册答案