
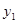 ���֣����·�
���֣����·� ��
��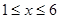 ����
���� ȡ������֮������ĺ�����ϵ���±���
ȡ������֮������ĺ�����ϵ���±����·� ���£� ���£� | 1 | 2 | 3 | 4 | 5 | 6 |
���͵���ˮ��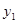 ���֣� ���֣� | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
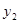 ���֣����·�
���֣����·� ��
��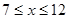 ����
���� ȡ������֮��������κ�����ϵʽ
ȡ������֮��������κ�����ϵʽ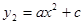 ����ͼ����ͼ��ʾ.1��6�£���ˮ������ÿ����ˮ�ķ���
����ͼ����ͼ��ʾ.1��6�£���ˮ������ÿ����ˮ�ķ���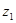 (Ԫ)���·�
(Ԫ)���·� ֮�����㺯����ϵʽ
֮�����㺯����ϵʽ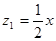 ������ҵ��������ÿ����ˮ�ķ���
������ҵ��������ÿ����ˮ�ķ���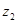 ��Ԫ�����·�
��Ԫ�����·� ֮�����㺯����ϵʽ
֮�����㺯����ϵʽ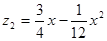 ��7��12�£���ˮ������ÿ����ˮ�ķ��þ�Ϊ2Ԫ������ҵ��������ÿ����ˮ�ķ��þ�Ϊ1.5Ԫ.
��7��12�£���ˮ������ÿ����ˮ�ķ��þ�Ϊ2Ԫ������ҵ��������ÿ����ˮ�ķ��þ�Ϊ1.5Ԫ.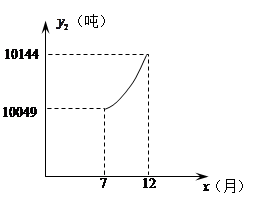
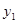 ��
��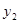 ��
�� ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ�� ��������ˮ�����ķ���ΪW��Ԫ���������W��
��������ˮ�����ķ���ΪW��Ԫ���������W�� ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ�� ��y2=x2��10000 ��2��
��y2=x2��10000 ��2��
 �ɷ�����������ϵ����
�ɷ�����������ϵ���� ����ͼ��֪��
����ͼ��֪�� �ɶ��κ���������㣨7,10049������12,10144�����������y2=x2��10000
�ɶ��κ���������㣨7,10049������12,10144�����������y2=x2��10000






| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
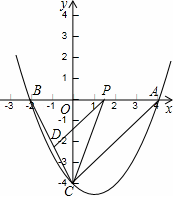
 ��x�����������A��B����y�ύ�ڵ�C��A������Ϊ��4��0����C�����꣨0����4����
��x�����������A��B����y�ύ�ڵ�C��A������Ϊ��4��0����C�����꣨0����4����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��ͼ�����
��ͼ����� .
.
 ��ֱ�������Σ�
��ֱ�������Σ�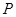 �ڵڶ����ޣ������������ϵ�һ���㣬����
�ڵڶ����ޣ������������ϵ�һ���㣬����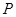 ��
��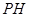 ��ֱ
��ֱ ���ڵ�
���ڵ� ����̽���Ƿ������
����̽���Ƿ������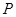 ��
�� ��
��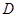 �������������
Ϊ������������� ���ƣ������ڣ����
���ƣ������ڣ����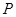 �������.�������ڣ���˵������.
�������.�������ڣ���˵������.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����B��3��0����C��0��3�����㣬����ΪA��
����B��3��0����C��0��3�����㣬����ΪA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ����ƽ��4����λ��������ƽ��1����λ�ɵõ�������
����ƽ��4����λ��������ƽ��1����λ�ɵõ�������
 ����������Բ�ľ�
����������Բ�ľ� ������Բ����.
������Բ����.| A���� | B���� | C���� | D���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��ͼ����ô���н��۴������ ��������
��ͼ����ô���н��۴������ �������� 
A���� ʱ�� ʱ�� �� �� �� �� | B���� ʱ�� ʱ��  �� �� |
C���� �� �� ʱ�� ʱ�� �� �� ����������� ����������� | D�����������߿��������� ƽ�Ƶõ� ƽ�Ƶõ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com