
【题目】在一个箱子里放有1个白球和2个红球,它们除颜色外其余都相同.
(1)从箱子里摸出1个球,是黑球,这属于什么事件;(填“必然”、“不可能”或“随机”)
(2)从箱子里摸出1个球,放回,摇匀后再摸出一个球,请利用树状图或表格计算,这样先后摸得的两个球都是红球的概率.
科目:初中数学 来源: 题型:
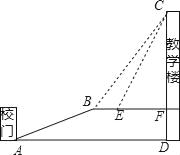
【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈![]() ,tan63.4°≈2)
,tan63.4°≈2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
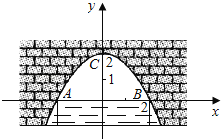
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在等腰直角△ABC中,分别以△ABC的三条边为斜边向△ABC外部作等腰直角△ABD、等腰直角△ACE、等腰直角△BCF,连结点D、E、F,则易知△DEF为等腰三角形.如果AB=AC=7,请直接写出△DEF的面积为 .
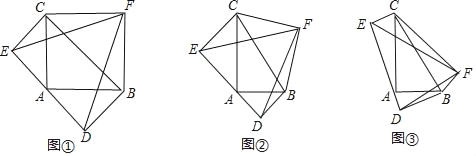
探究:如图②,Rt△ABC中,AB=14,AC=30,分别以△ABC的三条边为斜边向△ABC外部作等腰直角△ABD、等腰直角△ACE、等腰直角△BCF,连结点D、E、F,求△DEF的面积为多少.
拓展:如图③,Rt△ABC中,AB=14,AC=15,分别以△ABC的三条边为斜边向△ABC外部作Rt△ABD、Rt△ACE、Rt△BCF,且tan∠BCF=tan∠CAE=tan∠ABD=![]() ,连结点D、E、F,则△DEF的面积为 .
,连结点D、E、F,则△DEF的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把经过原点,顶点落在同一抛物线C上的所有抛物线称为抛物线C的派生抛物线.
(1)若y1=﹣x2+4x是抛物线C:y=ax2+2的派生抛物线,求a的值.
(2)证明:经过原点的抛物线y=﹣mx2+2mx+m﹣2是抛物线C:y=![]() x2+
x2+![]() 的派生抛物线;
的派生抛物线;
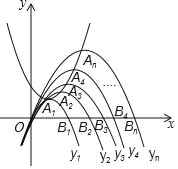
(3)如图,抛物线y1,y2,y3,y4…yn都是抛物线C:y=x2﹣2x+2的派生抛物线,其顶点A1,A2,A3,A4…An的横坐标分别是1、2、3、4…n,它们与x轴的另一个交点分别是B1,B2,B3,B4…Bn,与原点O构成的三角形分别为△OA1B1,△OA2B2,△OA3B3,△OA4B4…△OAnBn.
①请用含n的代数式表示抛物线yn的函数表达式;
②在这些三角形中,是否存在两个相似的三角形,若存在,请直接写出它们所对应的两个函数的表达式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数,若售价30元,能卖200台/月,若售价35元,能卖150台/月.
(1)求y与x的函数关系式.
(2)为清理库存,在不赔钱的情况下,售价定为多少元时,每月可获得最大销售量?
(3)如果想要每月获得2000元的利润,那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收物、易腐垃圾、有害垃圾和其他垃圾四大类. 现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶,投放正确的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣2(m+1)x+m2+5=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若原方程的两个实数根为x1、x2, 且满足x12+x22=|x1|+|x2|+2x1x2,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com