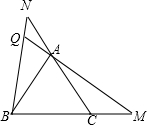
证明:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
又BM=CN,
∴△ABM≌△BCN;
(2)∵三角形ABC为等边三角形,
∴∠ABM=∠BCN=60°,AB=BC,又BM=CN,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
又∠BQM=∠ABQ+∠BAM=∠ABQ+∠CBN=∠ABC=60°;
(3)如图所示,
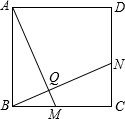
由题中条件可得Rt△ABM≌Rt△CBN,
∴∠BAM=∠CBN,
又∠BQM=∠ABQ+∠BAM=∠ABQ+∠CBN=∠ABC=90°.
分析:(1)由等边三角形的性质可得AB=BC,∠ABC=∠C=60°,再由题中BM=CN,即可得出结论;
(2)由(1)中可得∠BAM=∠CBN,再由∠BQM=∠ABQ+∠BAM=∠ABQ+∠CBN,即通过角之间的转化即可求解;
(3)求解过程与(1)、(2)相同,只不过把等边三角形改为正方形而已.
点评:本题主要考查了全等三角形的判定及性质以及一些等边三角形及正方形的性质,应熟练掌握.






 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案