
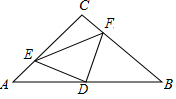
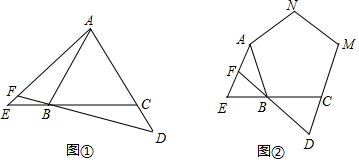
 ��ͼ���ڡ�ABC�У���C=90�㣬AC=BC=4��D��AB���е㣬E��F����ֱ���AC��BC�����˶�������E�����A��C�غϣ����ұ���AE=CF������DE��DF��EF���ڴ��˶��仯�Ĺ����У������н��ۣ�
��ͼ���ڡ�ABC�У���C=90�㣬AC=BC=4��D��AB���е㣬E��F����ֱ���AC��BC�����˶�������E�����A��C�غϣ����ұ���AE=CF������DE��DF��EF���ڴ��˶��仯�Ĺ����У������н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� �ٵ�EΪAC�е㣬FΪBC�е�ʱ���ı���CEDFΪ�����Σ�
�������渨��������CD����SAS������֤��CDF�͡�ADEȫ�ȣ��Ӷ���֤��EDF=90�㣬DE=DF�����ԡ�DFE�ǵ���ֱ�������Σ�
���ɢڡ�ADE�ա�CDF������S��ADE=S��CDF����ͨ�����������Ϳ���������ۣ�
�ܡ�DEF�ǵ���ֱ�������Σ�$\sqrt{2}$DE=EF����DF��BC��ֱ����DF��Сʱ��FEȡ��Сֵ2$\sqrt{2}$����ʱ��C���߶�EF�������룮
��� �⣺�ٵ�E��F�ֱ�ΪAC��BC�е�ʱ���ı���CDFE�������Σ�
�����ı���CEDF����Ϊ�����Σ���ѡ��ٴ���
����CD��
�ߡ�ABC�ǵ���ֱ�������Σ�
���DCB=��A=45�㣬CD=AD=DB��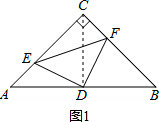
���ڡ�ADE�͡�CDF�У�
$\left\{\begin{array}{l}{AE=CF}\\{��A=��DCF}\\{AD=CD}\end{array}\right.$
���ADE�ա�CDF��SAS����
��ED=DF����CDF=��EDA��
�ߡ�ADE+��EDC=90�㣬
���EDC+��CDF=��EDF=90�㣬
���DFE�ǵ���ֱ�������Σ���ѡ�����ȷ��
�ۡߡ�ADE�ա�CDF��
��S��ADE=S��CDF��
��S�ı���CEDF=S��CED+S��CFD��
��S�ı���CEDF=S��CED+S��AED��
��S�ı���CEDF=S��ADC��
��S��ADC=$\frac{1}{2}$S��ABC=4��
���ı���CEDF������Ƕ�ֵ4��
���ı���CEDF����������Eλ�õĸı�������仯����ѡ��۴���
����C��EF�ľ���Ϊd��CF=x��
�ߡ�DEF�ǵ���ֱ�������Σ���D��EF�ľ���Ϊ$\frac{1}{2}$��
���ı���CEDF������Ƕ�ֵ4��
��S�ı���CEDF=S��CEF+S��FED=$\frac{EF}{2}$=4
d=$\frac{8}{EF}$����EFԽС�������Խ������ԽС��dԽ��
�ɹ��ɶ�����֪EF2=x2+��4-x��2=2��x-2��2+8��0��x��4��
��x=2ʱ��EFȡ��Сֵ=$\sqrt{8}$=2$\sqrt{2}$��
�����ã�d=$\sqrt{2}$����ѡ�����ȷ��
��ѡB��
���� ������Ҫ������ȫ�������ε��ж��������Լ������Ρ����������Ρ�ֱ�����������ʵ�֪ʶ������ͼ�����ø����֪�ı���CEDF���������������CMDN����ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
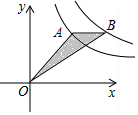 ��ͼ����ֱ������ϵ�У���A�Ƿ���������y=$\frac{2}{x}$ͼ���ڵ�һ�����ϵ�һ�㣬����A��x���ƽ���߽�����������y=$\frac{4}{x}$ͼ���ڵ�B������A�ĺ�����������ʱ�����ABO������仯����ǣ�������
��ͼ����ֱ������ϵ�У���A�Ƿ���������y=$\frac{2}{x}$ͼ���ڵ�һ�����ϵ�һ�㣬����A��x���ƽ���߽�����������y=$\frac{4}{x}$ͼ���ڵ�B������A�ĺ�����������ʱ�����ABO������仯����ǣ�������| A�� | �ȼ�С������ | B�� | ��������С | C�� | �������� | D�� | ���ֲ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com