
 如图,点P是y轴正半轴上的一动点,过点P作AB∥x轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象于点A,B,连接OA,OB,则以下结论:①AP=2BP;②∠AOP=2∠BOP;③△AOB的面积为定值;④△AOB是等腰三角形,其中一定正确的有( )个.
如图,点P是y轴正半轴上的一动点,过点P作AB∥x轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象于点A,B,连接OA,OB,则以下结论:①AP=2BP;②∠AOP=2∠BOP;③△AOB的面积为定值;④△AOB是等腰三角形,其中一定正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设P的坐标为(0,m),过点A、B作AC⊥x轴于点C、BD⊥x轴于点D,分别求出C、D的坐标,根据OA、OB、AB的长度即可判断.
解答 解:设P的坐标为(0,b),b>0
过点A、B作AC⊥x轴于点C、BD⊥x轴于点D,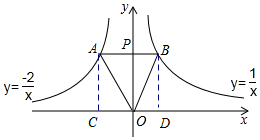 令y=m分别代入y=-$\frac{2}{x}$,y=$\frac{1}{x}$,
令y=m分别代入y=-$\frac{2}{x}$,y=$\frac{1}{x}$,
∴A($-\frac{2}{b}$,b),B($\frac{1}{b}$,b)
∴AB=$\frac{3}{b}$,AP=$\frac{2}{b}$,BP=$\frac{1}{b}$,
∴AP=2AB,故①正确;
tan∠AOP=$\frac{AP}{OP}$=$\frac{2}{{b}^{2}}$,tan∠BOP=$\frac{BP}{OP}$=$\frac{1}{{b}^{2}}$,
∴tan∠AOP=2tan∠BOP,但∠AOP≠BOP,故②错误;
△ABO的面积为:$\frac{1}{2}$AB•OP=$\frac{1}{2}$×$\frac{3}{b}$×b=$\frac{3}{2}$,故③正确;
由勾股定理可知:OA2=$\frac{4}{{b}^{2}}$+b2,OB2=b2+$\frac{1}{{b}^{2}}$,
∵AB2=$\frac{9}{{b}^{2}}$,
∴OA、OB、OA三边不一定相等,故④错误;
故选(B)
点评 本题考查反比例函数 的性质,解题的关键是熟练运用反比例函数的性质,勾股定理等知识,本题数中等题型.


科目:初中数学 来源: 题型:填空题
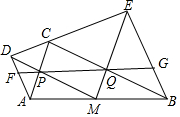 如图,在Rt△ABC中,∠ACB=90°,分别以AC、AB为斜边向△ABC外作等腰直角△ACD和等腰直角△BCE,取AB的中点M,连接MD,ME分别交AC、BC于点P、Q,直线PQ分别交AD、BE于点F、G.有以下结论:①△MDE是等腰直角三角形;②PQ=PF+QG;③△APF∽△EQG;④S△ACD+S△BCE=S△ABC.
如图,在Rt△ABC中,∠ACB=90°,分别以AC、AB为斜边向△ABC外作等腰直角△ACD和等腰直角△BCE,取AB的中点M,连接MD,ME分别交AC、BC于点P、Q,直线PQ分别交AD、BE于点F、G.有以下结论:①△MDE是等腰直角三角形;②PQ=PF+QG;③△APF∽△EQG;④S△ACD+S△BCE=S△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $±\sqrt{\frac{4}{9}}=\frac{2}{3}$ | B. | $±\sqrt{\frac{4}{9}}=±\frac{2}{3}$ | C. | $\sqrt{\frac{4}{9}}=\frac{2}{3}$ | D. | $\sqrt{\frac{4}{9}}=±\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是87.5米.
甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是87.5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com