
分析 先对除数的分子分母 进行因式分解,然后利用乘法分配即可求出答案.
解答 解:原式=($\frac{1}{a-1}$-$\frac{1}{{a}^{2}-1}$)×$\frac{{a}^{2}-1}{{a}^{2}-a}$
=($\frac{1}{a-1}$-$\frac{1}{{a}^{2}-1}$)×$\frac{(a+1)(a-1)}{a(a-1)}$
=($\frac{1}{a-1}$-$\frac{1}{{a}^{2}-1}$)×$\frac{a+1}{a}$
=$\frac{1}{a-1}$×$\frac{a+1}{a}$-$\frac{1}{(a-1)(a+1)}$×$\frac{a+1}{a}$
=$\frac{a+1}{a(a-1)}$-$\frac{1}{a(a-1)}$
=$\frac{1}{a-1}$
点评 本题考查分式的混合运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.


科目:初中数学 来源: 题型:解答题
 尺规作图并说明作图依据
尺规作图并说明作图依据查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
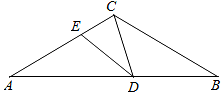 如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.
如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
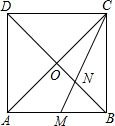 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为( )
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
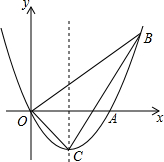 如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com