
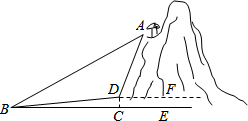
 我市AAAA景区有一处景观奇异的望天洞,D点是望天洞的入口,游人从入口进洞后,可经山洞到山顶的出口亭A处观光,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD的长为120米,坡角为∠DBC=10°,在B出测得A的仰角∠ABC=40°,在D出测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.
我市AAAA景区有一处景观奇异的望天洞,D点是望天洞的入口,游人从入口进洞后,可经山洞到山顶的出口亭A处观光,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD的长为120米,坡角为∠DBC=10°,在B出测得A的仰角∠ABC=40°,在D出测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.分析 (1)利用点D处的周角即可求得∠ADB的度数;
(2)首先分析图形,根据题意构造直角三角形.本题涉及到两个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
解答 解:(1)∵DC⊥CE,
∴∠BCD=90°,
又∵∠DBC=10°,
∴∠BDC=80°,
∵∠ADF=85°,
∴∠ADB=360°-80°-90°-85°=105°;
(2)过点D作DG⊥AB于点G.
在Rt△GDB中,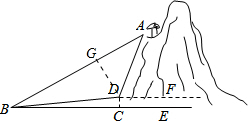
∠GBD=40°-10°=30°,
∴∠BDG=90°-30°=60°,
又∵BD=100,
∴GD=BD=100×$\frac{1}{2}$=50,
∴GB=BD×cos30°=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$,
在Rt△ADG=105°-60°=45°,
∴GD=GA=50,
∴AB=AG+GB=50+50$\sqrt{3}$,
答:索道长(50+50$\sqrt{3}$)米.
点评 本题考查仰角的定义及直角三角形的解法,首先构造直角三角形,再借助角边关系、三角函数的定义解题,正确的构造出直角三角形是解题关键.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
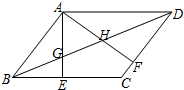 如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于GH.
如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于GH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C.
如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com