
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y= x的图象的交点
x的图象的交点 为C(m,4).
为C(m,4).
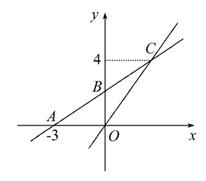
(1)求一次函数y=kx+b的解析式.
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,求点D的坐标.
(1)∵点C(m,4)在直线y= x上,
x上,
∴4= m,
m,
解得m=3.
∵点A(-3,0)与C(3,4)在直线y=kx+b(k≠0)上,
∴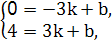 解得
解得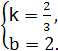
∴一次函数的解析式为y= x+2.
x+2.
(2)如图,过点D1作D1E⊥y轴于点E,过点D2作D2F⊥x轴于点F,
∵点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,
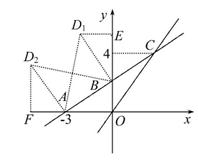
∴AB=BD1,AB=AD2,
∵∠D1BE+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠D1BE.
∵在△BED1和△AOB中,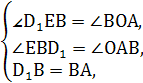
∴△BED1≌△AOB(AAS),
∴BE=AO=3,D1E=BO=2,
即可得出点D的一个坐标为(-2,5),同理可得出:△D2FA≌△AOB,
∴FA=OB=2,D2F=AO =3,
=3,
∴点D的另一个坐标为(-5,3),
综上所述:点D的坐标为(-2,5)或(-5,3).


科目:初中数学 来源: 题型:
有两块试验田,原来可产花生470千克,改用良种后共产花生532千克,已知第一块田的产量比原来增加16%,第二块田的产量比原来增加10%,问这两块试验田改用良种后,各增产花生多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
体育课上,20人一组进行足球比赛,每人射点球5次,已知某 一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是
一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是
( )
| 进球数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 5 | x | y | 3 | 2 |
A.y=x+9与y= x+
x+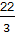
B.y=-x+9与y=
 x+
x+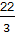
C.y=-x+9与y=- x+
x+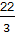
D.y=x+9与y=- x+
x+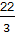
查看答案和解析>>
科目:初中数学 来源: 题型:
有一根长40mm的金属棒,欲将其截成x根7mm长的小段和y根9mm长的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.x=1,y=3 B.x=3,y=2
C.x=4,y=1 D.x=2,y=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com