
【题目】如图,8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.将△ABC经过一次平移后得到△A′B′C′,点B′是点B的对应点.
(1)△ABC的面积是 ;
(2)画出平移后得到的△A′B′C′;
(3)画出△ABC的高线CD.

科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt ABC中,![]() ,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.
,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE与射线AF交于点G.若OE将∠BOA分成1︰2两部分,AF平分∠BAD,∠ABO=![]() (30°<
(30°<![]() <90°) ,则∠OGA的度数为(用含
<90°) ,则∠OGA的度数为(用含![]() 的代数式表示)____________________.
的代数式表示)____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有足够多的长方形和正方形卡片,如下图:

(1)如果选取1号、2号、3号卡片分别为l张、1张、2张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形(所画图形大小和原图保持一致),并用等式表示拼图前后面积之间的关系:
(2)小明用类似方法解释分解因式a2+5ab+4b2,请画图说明小明的方法(所画图形大小和原图保持一致),并写出分解因式的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,∠E﹣∠F=36°,则∠E=( )

A.82°B.84°C.97°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产一种新型生物医药产品,生产成本为2万元/ 吨,每月生产能力为12吨,且生产出的产品都能销售出去.这种产品部分内销,另一部分外销(出口),内销与外销的单价![]() (单位:万元/吨)与销量的关系分别如图1,图2.
(单位:万元/吨)与销量的关系分别如图1,图2.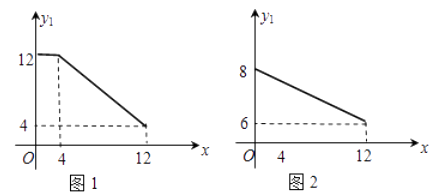
(1)如果该公司内销数量为x(单位:吨),内、外销单价分别为y 1 , y 2 ,求, ![]() 关于x的函数解析式;
关于x的函数解析式;
(2)如果该公司内销数量为x(单位:吨),求内销获得的毛利润 ![]() 关于x的函数解析式;
关于x的函数解析式;
(3)请设计一种销售方案,使该公司本月能获得最大毛利润,并求出毛利润的最大值.(毛利润=销售收入-生产成本).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com