
| A. | 3m2-6mn+3n2=3(m-n)2 | B. | x2b+ab2+ab=ab(a+b+1) | ||
| C. | mx2-4m=m(x-2)(x+2) | D. | x2+12x+36=(x+6)2 |
科目:初中数学 来源: 题型:解答题
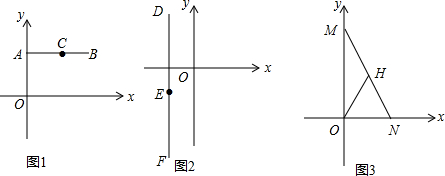
 在同一坐标系中画出了三个一次函数的图象:
在同一坐标系中画出了三个一次函数的图象:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度随时间的变化规律如图所示(图中OABC为一折线),这个容器的形状是图中的哪一个( )
匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度随时间的变化规律如图所示(图中OABC为一折线),这个容器的形状是图中的哪一个( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我市某中学课外活动小组的同学要测量海河某段流域的宽度,小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处188米远的B处测得∠CBD=30°,根据这些数据计算出这段流域的河宽和BC的长.
如图,我市某中学课外活动小组的同学要测量海河某段流域的宽度,小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处188米远的B处测得∠CBD=30°,根据这些数据计算出这段流域的河宽和BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 双胞胎兄弟小明和小亮在同一班读书,周五16:00时放学后,小明和同学走路回家,途中没有停留,小亮骑车回家,他们各自与学校的距离S(米)与用去的时间t(分钟)的关系如图所示,根据图象提供的有关信息,下列说法中错误的是( )
双胞胎兄弟小明和小亮在同一班读书,周五16:00时放学后,小明和同学走路回家,途中没有停留,小亮骑车回家,他们各自与学校的距离S(米)与用去的时间t(分钟)的关系如图所示,根据图象提供的有关信息,下列说法中错误的是( )| A. | 兄弟俩的家离学校1000米 | |
| B. | 他们同时到家,用时30分钟 | |
| C. | 小明的速度为50米/分钟 | |
| D. | 小亮中间停留了一段时间后,再以80米/分钟的速度骑回家 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com