
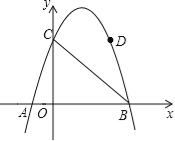
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.
(1)求tan∠DBC的值;
(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
【答案】(1)tan∠DBC=![]() ;
;
(2)P(﹣![]() ,
,![]() ).
).
【解析】
(1)连接CD,过点D作DE⊥BC于点E.利用抛物线解析式可以求得点A、B、C、D的坐标,则可得CD//AB,OB=OC,所以∠BCO=∠BCD=∠ABC=45°.由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4![]() ,BE=BC﹣DE=
,BE=BC﹣DE=![]() .由此可知tan∠DBC=
.由此可知tan∠DBC=![]() ;
;
(2)过点P作PF⊥x轴于点F.由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC,利用(1)中的结果得到:tan∠PBF=![]() .设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知
.设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知![]()
![]() ,通过解方程求得点P的坐标为(﹣
,通过解方程求得点P的坐标为(﹣![]() ,
,![]() ).
).
(1)令y=0,则﹣x2+3x+4=﹣(x+1)(x﹣4)=0,
解得 x1=﹣1,x2=4.
∴A(﹣1,0),B(4,0).
当x=3时,y=﹣32+3×3+4=4,
∴D(3,4).
如图,连接CD,过点D作DE⊥BC于点E.

∵C(0,4),
∴CD//AB,
∴∠BCD=∠ABC=45°.
在直角△OBC中,∵OC=OB=4,
∴BC=4![]() .
.
在直角△CDE中,CD=3.
∴CE=ED=![]() ,
,
∴BE=BC﹣DE=![]() .
.
∴tan∠DBC=![]() ;
;
(2)过点P作PF⊥x轴于点F.
∵∠CBF=∠DBP=45°,
∴∠PBF=∠DBC,
∴tan∠PBF=![]() .
.
设P(x,﹣x2+3x+4),则![]() ,
,
解得 x1=﹣![]() ,x2=4(舍去),
,x2=4(舍去),
∴P(﹣![]() ,
,![]() )..
)..


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,﹣1).

(1)以点C为中心,把△ABC逆时针旋转90°,请在图中画出旋转后的图形△A′B′C,点B′的坐标为________;
(2)在(1)的条件下,求出点A经过的路径![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
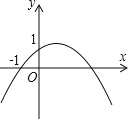
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
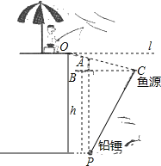
【题目】如图所示,老张利用国庆假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6m,微风吹来时,假设铅锤P不动,鱼漂移动了一段距离BC,且项場恰好与水面平齐(即PAPC,水平线1与OC夹角a=8°(点A在OC上,则铅锤P处的水深h为( )(参考数据:sin8°=![]() ,cos8°=
,cos8°=![]() ,tan8°=
,tan8°=![]() )
)
A.150cmB.144cmC.111cmD.105cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC,OC=2,抛物线y=ax2+c过A,B,C三点,D为抛物线上一点,连接BD且tan∠DBC=![]() .
.

(1)求直线BD和抛物线所表示的函数解析式.
(2)如果在抛物线上有一点E,使得S△EBC=S△ABD,求这时E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.

(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,交AC于点E.
(1)求证:BD=CD.
(2)若弧DE=50°,求∠C的度数.
(3)过点D作DF⊥AB于点F,若BC=8,AF=3BF,求弧BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展.据调查,太原市某家小型“大学生自主创业”的快递公司,今年九月份与十一月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递业务员能否完成今年十二月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近代统计学的发展起源于二十世纪初,它是在概率论的基础上发展起来的,但统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我国人口、钱粮、水文、天文、地震等资料的记录.现代数理统计的奠基人是英国数学家和生物学家费希尔,毕业于剑桥大学,长期在农业试验站做生物实验.费尔希在高等植物基因性状研究实验中,从若干紫花与白花中各随机抽取20株测量高度(植株正常高度![]() 的取值范围为
的取值范围为![]() ),过程如下:
),过程如下:
收集数据(单位:![]() ):
):
紫花:42,42,28,54,29,52,44,36,39,49,33,40,35,52,29,32,51,55,42,38
白花植株高度为![]() 的数据有:35,37,37,38,39,40,42,42
的数据有:35,37,37,38,39,40,42,42
整理数据:
数据分为六组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
组别 |
|
|
|
|
|
|
紫花数量 | 3 | 2 |
| 5 | 1 | 5 |

分析数据:
植株 | 平均数 | 众数 | 中位数 | 方差 |
紫花 | 41.1 | 42 | 41 | 8.8 |
白花 | 40.25 | 43 |
| 7.2 |
应用数据:
(1)请写出表中![]() ,
,![]() ;
;
(2)估计500株紫花中高度正常的有多少株?
(3)结合上述数据信息,请判断哪种花长势更均匀,并说明理由(一条理由即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com