
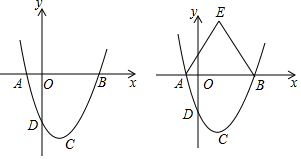
分析 (1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据平行四边形的判定,可得H是平行四边形对角线的交点,根据平行四边形的性质,可得DH的直线平分平行四边形;根据解方程组,可得答案;
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得HE的长,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案.
解答 解:(1)将(2,-3)、(-1,0)代入函数解析式,得
$\left\{\begin{array}{l}{4+2b+c=-3}\\{1-b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
抛物线的函数表达为y=x2-2x-3,
y=(x-1)2-4,即顶点C坐标为(1,-4)
(2)如图1 ,当x=0时,y=-3,即D点坐标为(0,-3)
,当x=0时,y=-3,即D点坐标为(0,-3)
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,即A(-1,0),B(3,0),
由题意,得HE=HC,HA=HB,即ACBE是平行四边形,F点坐标为(1,0),
DF的解析式为y=kx+b,将D,F代入函数解析式,得$\left\{\begin{array}{l}{k+b=0}\\{b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=-3}\end{array}\right.$,
DF的解析式为y=3x-3,
联立DF与抛物线,得
$\left\{\begin{array}{l}{y={x}^{2}-2x-3}\\{y=3x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=-3}\end{array}\right.$(舍),$\left\{\begin{array}{l}{x=5}\\{y=12}\end{array}\right.$,即F点坐标(5,12);
(3)如图2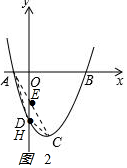 ,设H点坐标为(m,m2-2m-3)设AC的解析式为y=kx+b,将A,C代入,得$\left\{\begin{array}{l}{-k+b=0}\\{k+b=-4}\end{array}\right.$,
,设H点坐标为(m,m2-2m-3)设AC的解析式为y=kx+b,将A,C代入,得$\left\{\begin{array}{l}{-k+b=0}\\{k+b=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
即AC的解析式为y=-2x-2,
设H点坐标为(m,m2-2m-3),E(m,-2m-2,),
HE=-2m-2-(m2-2m-3)=-m2+1,
S△HCA=$\frac{1}{2}$AC•(xC-xA)=$\frac{1}{2}$(-m2+1)[1-(-1)]=-m2+1,
当m=0时,S△HCA最大=1,m=0时,m2-2m-3=-3,即H点坐标为(0,-3).
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用平行四边形的判定与性质得出过对角线交点的直线平分平行四边形是解题关键;解(3)的关键是利用三角形的面积得出二次函数是解题关键,又利用了二次函数的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 6.767×1012 | B. | 6.767×1013 | C. | 67.67×1012 | D. | 6.767×1014 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
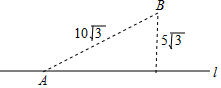 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5$\sqrt{3}$千米的地方有一居民点B,A、B的直线距离是10$\sqrt{3}$千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{3}{8}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5$\sqrt{3}$千米的地方有一居民点B,A、B的直线距离是10$\sqrt{3}$千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{3}{8}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=45°;③BG=GC;④AG∥CF.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=45°;③BG=GC;④AG∥CF.其中正确结论的个数是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩分数 | 27 | 28 | 30 |
| 人数 | 4 | 3 | 1 |
| A. | 28 27.5 27.75 | B. | 27 27.5 27.75 | ||
| C. | 28 27 27.7 | D. | 27 28 27.75 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com