
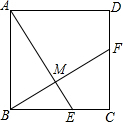
 如图,正方形ABCD中,点E、F分别是边BC、CD上的点,且BE=CF,求证:
如图,正方形ABCD中,点E、F分别是边BC、CD上的点,且BE=CF,求证:分析 (1)根据正方形的性质可得AB=BC,∠ABE=∠BCF,然后利用“边角边”证明△ABE和△BCF全等,即可得出结论;
(2)根据全等三角形对应边相等可得AE=BF,全等三角形对应角相等可得∠BAE=∠CAF,然后求出∠BAE+∠ABF=∠ABC=90°,判断出AE⊥BF.
解答 证明:(1)在正方形ABCD中,AB=BC,∠ABE=∠BCF,
在△ABE和△BCF中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABE=∠BCF}&{\;}\\{BE=CF}&{\;}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴AE=BF;
(2)∵△ABE≌△BCF,
∴∠BAE=∠CAF,
∴∠BAE+∠ABF=∠CAF+∠ABF=∠ABC=90°,
∴AE⊥BF.
点评 本题考查了正方形的性质,全等三角形的判定与性质,确定出AE与BF所在的三角形并证明三角形全等是解题的关键.


科目:初中数学 来源: 题型:解答题
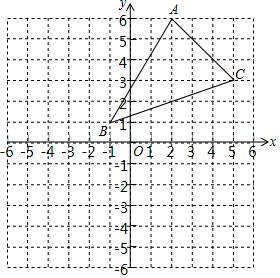 如图,三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合.
如图,三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
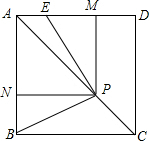 如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
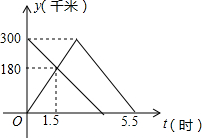 甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.
甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
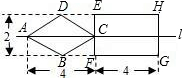 如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )
如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )| A. | 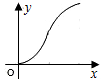 | B. | 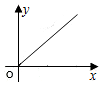 | C. | 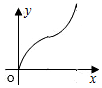 | D. | 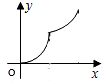 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com