
 如图,AC分别切⊙O于D、E,作OQ⊥BC交⊙O于P,连DP、EP交BC于G、F,AF、AG分别交DG、EF于M、N.求证:OQ⊥MN.
如图,AC分别切⊙O于D、E,作OQ⊥BC交⊙O于P,连DP、EP交BC于G、F,AF、AG分别交DG、EF于M、N.求证:OQ⊥MN. 分析 连接OD、OE.首先证明∠CEF=∠CFE,推出CF=CE,同理可证BD=BG,由梅涅劳斯定理可知$\frac{AN}{NG}$•$\frac{GF}{CF}$•$\frac{CE}{AE}$=1,$\frac{AM}{MF}$•$\frac{FG}{BG}$•$\frac{BD}{AD}$=1,又因为AD=AE.CE=CF,BD=BG,推出$\frac{AN}{NG}$=$\frac{AM}{NF}$,推出MN∥BC,由OQ⊥BC,即可推出OQ⊥MN.
解答 证明:连接OD、OE.
∵AB、AC是⊙O的切线,
∴OD⊥AB,OE⊥AC,∵OQ⊥BC,
∴∠OEC=∠OQC=90°,
∴∠QOE+∠C=180°,
∴∠QOE=180°-∠C,
∵OE=OP,
∴∠OEP=∠OPE=$\frac{180-∠QOE}{2}$=$\frac{1}{2}$∠C,
∴∠FPQ=∠OPE=$\frac{1}{2}$∠C,
∴∠EFC=90°-∠FPQ=90°-$\frac{1}{2}$∠C,
∴∠CEF=180°-∠EFC-∠C=90°-$\frac{1}{2}$∠C,
∴∠CEF=∠CFE,
∴CF=CE,同理可证BD=BG,
由梅涅劳斯定理可知$\frac{AN}{NG}$•$\frac{GF}{CF}$•$\frac{CE}{AE}$=1,$\frac{AM}{MF}$•$\frac{FG}{BG}$•$\frac{BD}{AD}$=1,
∵AD=AE.CE=CF,BD=BG,
∴$\frac{AN}{NG}$=$\frac{AM}{NF}$,
∴MN∥BC,
∵OQ⊥BC,
∴OQ⊥MN.
点评 本题考查圆综合题,切线的性质、等腰三角形的判定和性质、梅涅劳斯定理等知识,解题的关键是证明CF=CE,BD=BG,本题的突破点是应用由梅涅劳斯定理,推出$\frac{AN}{NG}$=$\frac{AM}{NF}$,推出MN∥BC,属于竞赛题目.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
| 萨尔图区 | 让葫芦区 | 红岗区 | |
| 运往肇东的费用(元/吨) | 220 | 200 | 200 |
| 运往肇源的费用(元/吨) | 250 | 220 | 210 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l的解析式为y=-$\frac{4}{3}$x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).
如图,直线l的解析式为y=-$\frac{4}{3}$x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
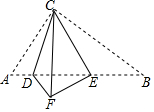 如图,在△ACB中,∠ACB=90°,∠A=45°,沿图中CD翻折,将△ACD折到△FCD,然后沿CE将△CEB翻折,使CB与CF重合,观察这个图形.
如图,在△ACB中,∠ACB=90°,∠A=45°,沿图中CD翻折,将△ACD折到△FCD,然后沿CE将△CEB翻折,使CB与CF重合,观察这个图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com