
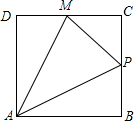
 如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )
如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )| A. | 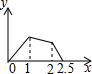 | B. | 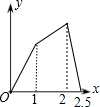 | C. | 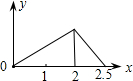 | D. | 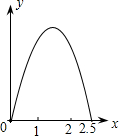 |
分析 本题是一个分段函数,分点P在AB,BC和CM上得到三个一次函数,然后由一次函数的图象与性质确定选项.
解答 解:当点P在AB上时,如图:
y=$\frac{1}{2}$x (0≤x≤1).
当点P在BC上时,如图:
PB=x-1,PC=2-x,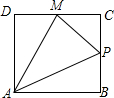
y=S正方形ABCD-S△ADM-S△ABP-S△PCM
=1-$\frac{1}{4}$-$\frac{1}{2}$(x-1)-$\frac{1}{2}$•$\frac{1}{2}$•(2-x)=-$\frac{1}{4}$x+$\frac{3}{4}$,
∴y=-$\frac{1}{4}$x+$\frac{3}{4}$(1<x≤2)
当点P在CM上时,如图,MP=2.5-x,
∴y=$\frac{1}{2}$(2.5-x)=-$\frac{1}{2}$x+$\frac{5}{4}$.(2<x≤2.5)
得到的三个函数都是一次函数,由一次函数的图象与性质可以确定y与x的图形.
只有A的图象是三个一次函数,且在第二段上y随x的增大而减小,
故选:A.
点评 本题考查的是动点问题的函数图象,分别考虑点O在AB,BC和CM上,由三角形的面积公式得到三个一次函数,然后由一次函数的图象与性质得到y与x的图象.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
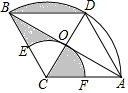 如图,菱形ACBD中,AB与CD交于点O,∠ACB=120°,以C为圆心、AC为半径作弧AB,再以C为圆心,CO为半径作弧EF分别交AC于点F、BC于点E,若CB=2,则图中阴影部分的面积为( )
如图,菱形ACBD中,AB与CD交于点O,∠ACB=120°,以C为圆心、AC为半径作弧AB,再以C为圆心,CO为半径作弧EF分别交AC于点F、BC于点E,若CB=2,则图中阴影部分的面积为( )| A. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{3}$-$\frac{1}{2}$ | C. | $\frac{2π}{3}$-$\frac{1}{2}$ | D. | π-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
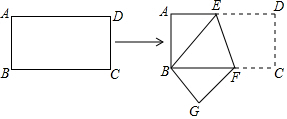 如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其折叠,使点D与点B重合.
如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其折叠,使点D与点B重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com