
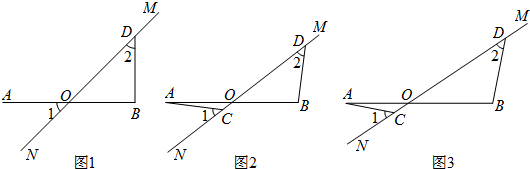
分析 (1)先根据∠BOD和∠2的度数,判断DB与OB的数量关系以及位置关系,再得出AO与BD的数量关系与位置关系;
(2)先过点B作BE∥AC,通过判定△AOC≌△BOE,得到∠BED的度数,再根据∠BED和∠2的度数,判断DB与EB的数量关系以及位置关系,再得出AC与BD的数量关系与位置关系;
(3)先过点B作BE∥AC,根据△AOC∽△BOE,得出BE与AC的比值,再根据DB=BE,得出BD与AC的比值.
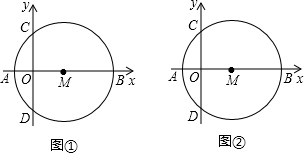
解答 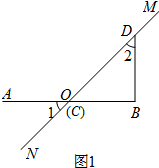 解:(1)如图1,当点C与点O重合时,∠1=∠DOB=45°
解:(1)如图1,当点C与点O重合时,∠1=∠DOB=45°
∵∠2=45°
∴DB=OB,且∠B=90°,即△BOD是等腰直角三角形
又∵AO=OB
∴AO=BD
∵∠B=90°
∴DB⊥AB,即DB⊥AO
故答案为:AO=BD;AO⊥BD
(2)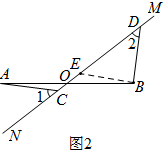 如图2,过点B作BE∥AC,交MN于E,则∠A=∠OBE
如图2,过点B作BE∥AC,交MN于E,则∠A=∠OBE
∵AO=BO,∠AOC=∠BOE
∴△AOC≌△BOE(ASA)
∴AC=BE,∠ACO=∠BEO
∴∠1=∠BED=45°
又∵∠2=45°
∴∠DBE=90°,且DB=BE,即△BED是等腰直角三角形
∴DB⊥BE,AC=DB
又∵BE∥AC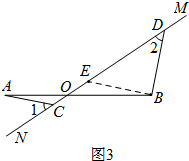
∴AC⊥BD
(3)如图3,过点B作BE∥AC,交MN于E,则△AOC∽△BOE
∴$\frac{BE}{AC}$=$\frac{BO}{AO}$=k,且∠ACO=∠BEO
∴∠1=∠BED=45°
又∵∠2=45°
∴DB=BE
∴$\frac{BD}{AC}$=k
点评 本题主要考查了旋转变换以及等腰直角三角形,解决问题的关键是掌握全等三角形的判定与性质,相似三角形的判定与性质.解答此类试题时,需要作平行线构造全等三角形或相似三角形进行求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
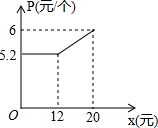 某企业接到一批零件的加工任务,要求在20天内完成,这批零件的出厂价为每个6元.为按时完成任务,该企业招收了新工人,在6天的培训期内,新工人小亮第x天能加工80x个零件,培训后小亮第x天内加工的零件个数为(50x+200)个.
某企业接到一批零件的加工任务,要求在20天内完成,这批零件的出厂价为每个6元.为按时完成任务,该企业招收了新工人,在6天的培训期内,新工人小亮第x天能加工80x个零件,培训后小亮第x天内加工的零件个数为(50x+200)个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 696×103 | B. | 69.6×104 | C. | 6.96×105 | D. | 6.96×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 通常加热到100℃时,水沸腾 | |
| B. | 抛掷2枚正方体骰子,都是6点朝上 | |
| C. | 经过有交通信号灯的路口,遇到红灯 | |
| D. | 任意画一个三角形,其内角和是360° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com