
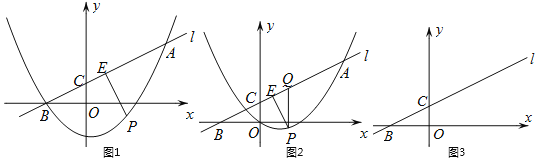
����Ŀ����ͼ1��������C1��y��![]() x2+ax+b��ֱ��l���ڵ�A(8��6)��B(��4��0)��ֱ��l��y����C����P��ֱ��l�·���������C1��һ���㣨����A��B���ص㣩��PE��AB�ڵ�E�����P�ĺ�����Ϊm��
x2+ax+b��ֱ��l���ڵ�A(8��6)��B(��4��0)��ֱ��l��y����C����P��ֱ��l�·���������C1��һ���㣨����A��B���ص㣩��PE��AB�ڵ�E�����P�ĺ�����Ϊm��
��1����������C1��ֱ��l�Ľ���ʽ��
��2����AB��3PE����m��ֵ��
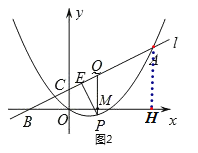
��3��������C1����ƽ��t����λ���õ�������C2����PΪ������C2��һ�㣬����x���·���PE��AB�ڵ�E������P��x��Ĵ��߽�x���ڵ�M����ֱ��l�ڵ�Q��
����ͼ2����t��4ʱ�����PQE�ܳ������ֵ��
�ڵ���P��������C2���˶�ʱ���߶�PM��QM��ֵ�ڲ��ϱ仯����![]() �����ֵΪ1�����ʱt���� ����ֱ��д���������
�����ֵΪ1�����ʱt���� ����ֱ��д���������
���𰸡���1��![]() �� y��
�� y��![]() x+2����2��m��2
x+2����2��m��2![]() ����3����8+
����3����8+![]() ����
����![]()
��������
��1������A��B���������y��![]() x2+ax+b��������������ߵĽ���ʽ����A��B�������y��mx+n���������ֱ��l�Ľ���ʽ��
x2+ax+b��������������ߵĽ���ʽ����A��B�������y��mx+n���������ֱ��l�Ľ���ʽ��
��2����ͼ1����A��AH��x�ᣬPF��x�ᣬEF��x�ύPF��F������ABH�ס�EPF����AB��3PE�����PF��4��EF��2�����P(m��![]() m2��
m2��![]() m��
m��![]() )����E(m��2��
)����E(m��2��![]() m2��
m2��![]() m+
m+![]() )����E����ֱ��l�Ľ���ʽ�������m��ֵ��
)����E����ֱ��l�Ľ���ʽ�������m��ֵ��
��3������t��4ʱ��ƽ�ƺ�Ľ���ʽC2Ϊ��y��![]() x2��
x2��![]() x����P(m��
x����P(m��![]() m2��
m2��![]() m)����Q(m��
m)����Q(m��![]() m+2)�����PQ�����ֵ����һ�����������PQE���ܳ����ֵ������д��ƽ�ƺ�Ľ���ʽ�����ú�m��t�Ĵ���ʽ��ʾ��PM��MQ�ij�����
m+2)�����PQ�����ֵ����һ�����������PQE���ܳ����ֵ������д��ƽ�ƺ�Ľ���ʽ�����ú�m��t�Ĵ���ʽ��ʾ��PM��MQ�ij�����![]() ��1���г�����ʽ���������ɺ�����ͼ���������t��ֵ��
��1���г�����ʽ���������ɺ�����ͼ���������t��ֵ��
�⣺��1������A��8��6����B����4��0�����룬
�ã�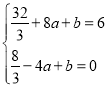 ��
��
��ã� ��
��
�������߽���ʽΪy��![]() x2��
x2��![]() x��
x��![]() ��
��
��ֱ��l�Ľ���ʽΪy��mx+n��
��A��B������룬�ã�![]() ��
��
��� ��
��
��ֱ��l�Ľ���ʽΪy��![]() x+2��
x+2��
��2����ͼ1����A��AH��x�ᣬPF��x�ᣬEF��x�ύPF��F��
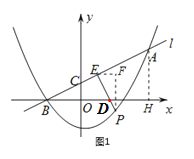
�ߡ�CBO+��BDE=90�㣬��P+��PDH=90�㣬
���CBD=��P��
�֡ߡ�F=��AHB=90�㣬
���ABH�ס�EPF��
��AB��3PE��
��BH��3PF��AH��3EF��
��BH��12��AH��6��
��PF��4��EF��2��
��P(m��![]() m2��
m2��![]() m��
m��![]() )����E(m��2��
)����E(m��2��![]() m2��
m2��![]() m+
m+![]() )��
)��
��E����ֱ��l����ã�m2��4m��2��0��
���m��2![]() ��
��
��3����A��AH��x����H��
����y��![]() x2��
x2��![]() x��
x��![]() =
=![]() ��
��
�൱t��4ʱ��ƽ�ƺ�Ľ���ʽC2Ϊ��y=![]() ��
��![]() x2��
x2��![]() x��
x��
��P(m��![]() m2��
m2��![]() m)����Q(m��
m)����Q(m��![]() m+2)��
m+2)��
��PQ��-![]() m2+2m+2����
m2+2m+2����![]() (m��6)2+8��
(m��6)2+8��
����m��6ʱ��PQȡ���ֵ8��
�ߡ�ABH=��EPQ����AHB=��PEQ��
����PQE�ס�ABH��
��EQ��PE��PQ��1��2��![]() ��
��
���PQE���ܳ����ֵ��PQ+PE+EQ��8+2��![]() +
+![]() ��8+
��8+![]() ��
��
����y��=![]() ��
��
��ƽ�ƺ�Ľ���ʽΪ��y��![]() x2��
x2��![]() +
+![]() ��
��
��PM����![]() m2+
m2+![]() ��
��![]() ��MQ��
��MQ��![]() m+2��
m+2��![]() ��1��
��1��
��-![]() m2+
m2+![]() ��
��![]() ��0��
��0��
����m����![]() ��t��1ʱ��-
��t��1ʱ��-![]() m2+
m2+![]() ��
��![]() �����ֵ0��
�����ֵ0��
��m��t��1����-![]() m2+
m2+![]() ��
��![]() ��0��
��0��
���t��![]() ��
��
�ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
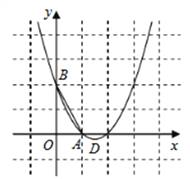
����Ŀ����֪���κ���y��ax2��bx��c��ͼ����ͼ��ʾ���Գ���Ϊֱ��x��1����λѧ��д��������������ۣ�

��1��ac>0��
��2������ax2��bx��c��0��������x1����1��x2��3��
��3��2a��b��0��
��4����x>1ʱ��y��x���������С��
��5��3a��2b��c>0
�����Ͻ����в���ȷ���У� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ���ͼ����֪������![]() ����
����![]() ��
��![]() ���㣬����Ϊ
���㣬����Ϊ![]() .
.
��1���������ߵĽ���ʽ��
��2����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��
��![]() ���ڵ�
���ڵ�![]() ��λ�ã�����������
��λ�ã�����������![]() ��ƽ�ƺ���
��ƽ�ƺ���![]() ����ƽ�ƺ�����ͼ��ĺ�����ϵʽ��
����ƽ�ƺ�����ͼ��ĺ�����ϵʽ��
��3���裨2����ƽ�ƺ�������������![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ������Ϊ
������Ϊ![]() ������
������![]() ��ƽ�ƺ���������ϣ�������
��ƽ�ƺ���������ϣ�������![]() �������
�������![]() �����2�������
�����2�������![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�ƻ������ס���������Ʒ��������Ʒ�Ľ����Ǽ�����Ʒ���۵ľ��ۣ���3600Ԫ����������ƷҪ�ȹ��������Ʒ����10����
��1����ס���������Ʒ�Ľ��۸��Ƕ���Ԫ��
��2�����̵�ƻ������ס���������Ʒ��80������������Ʒ�����������ڼ�����Ʒ������3����������Ʒ���ۼ۶�Ϊÿ��80Ԫ��������Ʒ���ۼ۶�Ϊÿ��70Ԫ�����ס���������Ʒ�������꣬����̵��ܻ�õ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
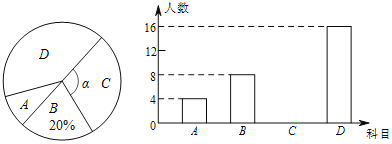
����Ŀ��Ϊ����ѧ��������������ѧϰ�ƻ�������������ѡ�Σ�A�鷨��B�滭��C������D�赸��Ϊ�˽�ѧ�������Ź��ε�ϲ���������ȫУ��Χ�������ȡ������ѧ�������ʾ����飨ÿ���������ѧ������ѡ�����ֻ��ѡ������һ�ţ��������ݽ��������������Ƴ�����������������ͳ��ͼ������ͼ��������Ϣ����������⣺
��1�����ε����ѧ�������� ���ˣ�����ͳ��ͼ�С����Ķ������� ����
��2���������ͳ��ͼ����������
��3�������У����2500��ѧ����������Ƹ�УD��ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
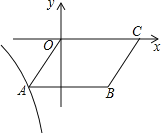
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�B��3����3����C��5��0������OC��CBΪ����ƽ���ı���OABC������y![]() ��x��0����ͼ����A��
��x��0����ͼ����A��
��1����k��ֵ��
��2��������A��ֱ��lƽ����ֱ��OB���ҽ�����y![]() ��x��0����ͼ���ڵ�D��
��x��0����ͼ���ڵ�D��
����ֱ��l�ı���ʽ��
�ڶ��壺�ᡢ�����궼�������ĵ�������㣮�Ǻ���y![]() ��x��0����ͼ���ڵ�A��D֮��IJ������߶�ADΧ�ɵ������߽磩ΪW����Ϻ���ͼ��ֱ��д������W�ڣ����߽磩�����������
��x��0����ͼ���ڵ�A��D֮��IJ������߶�ADΧ�ɵ������߽磩ΪW����Ϻ���ͼ��ֱ��д������W�ڣ����߽磩�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı��� ABCD �У�AE ƽ�֡�BAD ���� BC �� E��DF ƽ�֡�ADC ���� BC �� F���� AD=11��EF=5���� AB= ___��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
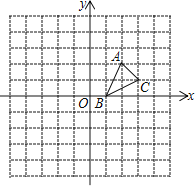
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��ABC�Ķ�����ڸ���ϣ��������������ֱ�ΪA��2��2����B��1��0����C��3��1��
��1������ABC����x������ԳƱ任�á�A1B1C1�����C1������Ϊ ��
��2������ABC��ԭ��O����ʱ�뷽����ת90��á�A2B2C2�����C2������Ϊ ��
��3���ڣ�1����2���Ļ����ϣ�ͼ�еġ�A1B1C1����A2B2C2�����ĶԳ�ͼ�Σ��Գ����ĵ�����Ϊ ��
��4�����Ե�D��A��C��BΪ������ı���Ϊ���Σ�ֱ��д����D������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̳�����A��B�����ͺż����������ּ������Ľ����۸�ֱ�Ϊÿ̨30Ԫ��40Ԫ. �̳�����5̨A�ͺź�1̨B�ͺż��������ɻ�����76Ԫ������6̨A�ͺź�3̨B�ͺż��������ɻ���120Ԫ.
��1�����̳�����A��B�����ͺż����������ۼ۸�ֱ��Ƕ���Ԫ��������=���ۼ۸��������۸�
��2���̳����ò�����2500Ԫ���ʽ�A��B�����ͺż�������70̨����������Ҫ����A�ͺŵļ���������̨��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com