
【题目】如图,在□ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
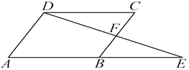
A. ∠E=∠CDF B. BE=CD C. ∠ADE=∠BFE D. BE=2CF
【答案】D
【解析】
先根据平行四边形的性质可得CD∥AB,AD∥BC,且CD=AB,再根据平行线的性质可得∠E=∠CDF,∠ADE=∠BFE;再证明△DCF≌△EBF可得CF=BF=![]() BC,根据题意不能证明BC=BE,因此BE不一定等于2CF.
BC,根据题意不能证明BC=BE,因此BE不一定等于2CF.
∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB, AD∥BC,
∴∠E=∠CDF,(故A成立);
∵BE=AB
∴BE=CD, (故B成立);
∵AD∥BC,
∴∠ADE=∠BFE (故C成立);
在△CDF和△BEF中,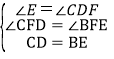
∴△DCF≌△EBF(AAS),
∴CF=BF=![]() BC,
BC,
∴BC=2CF
∵BC不一定等于BE,
∴2CF不一定等于BE,(故D不一定成立);
故选:D.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为2,a2+1,则点P所在的象限是____;以方程组![]() 的解为坐标的点x,y在平面直角坐标系中的位置是__________;在平面直角坐标系中,如果mn>0,请写出点m,|n|可能在的所有象限:____________.
的解为坐标的点x,y在平面直角坐标系中的位置是__________;在平面直角坐标系中,如果mn>0,请写出点m,|n|可能在的所有象限:____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
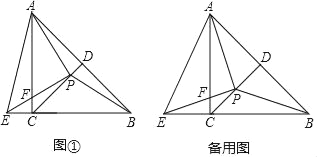
【题目】如图①,在等腰Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D.点P为线段CD上一点(不与端点C、D重合),PE⊥PA,PE与BC的延长线交于点E,与AC交于点F,连接AE、AP、BP.
(1)求证:AP=BP;
(2)求∠EAP的度数;
(3)探究线段EC、PD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+
x2+ ![]() x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,
x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6, ![]() )在抛物线上,直线AC与y轴交于点D.
)在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m,求AN的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
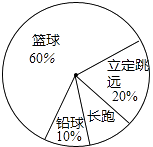
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为个;进球数的中位数为个,众数为个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD= 3,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,PE+PB的最小值 ______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N.若BM+CN=7,则MN的长为( )

A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com