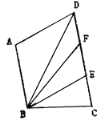
【题目】如图,AB∥CD,点E为CD上一点,连接BE,AD∥BE,连接BD,BD平分∠ABE,BF平分∠ABC交CD于点F, ∠ABC=100°，∠DBF=14°,∠ADC的度数为_______°.
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目：初中数学 来源： 题型：
【题目】问题：已知方程
，求一个一元二次方程，使它的根分别是已知方程根的2倍．
解：设所求方程的根为y，则
，所以
．
把
代入已知方程，得
．
化简，得： 
．
这种利用方程根的代替求新方程的方法，我们成为“换根法”，请用阅读材料提供的“换根法”求新方程
要求：把所求方程化成一般形式
；
(1)已知方程
，求一个一元二次方程，使它的根分别是已知方程根的相反数．
(2)已知关于x的一元二次方程
有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．
查看答案和解析>>
科目：初中数学 来源： 题型：
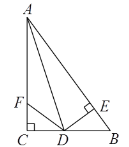
【题目】如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，且BD=DF．
（1）求证：CF=EB；
（2）试判断AB与AF，EB之间存在的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的，如果规定向东为正，向西为负，他这天上午所接六位乘客的行车里程（单位：
）如下：
，
，
，
，
，，
问：（1）将最后一位乘客送到目的地时，小李在什么位置？
（2）若汽车耗油量为
（升/千米），这天上午小李接送乘客，出租车共耗油多少升？
（3）若出租车起步价为8元，起步里程为
（包括），超过部分每千米1.2元，问小李这天上午共得车费多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图中的折线ABC表示某汽车的耗油量y(L/km)与速度x(km/h)之间的函数关系(30≤x≤120)．已知线段BC表示的函数关系中，该汽车的速度每增加1km/h，耗油量增加0.002L/km．
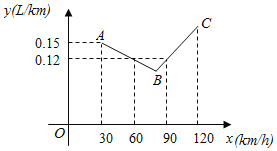
（1）当30≤x≤120时，求y与x之间的函数表达式；
（2）该汽车的速度是多少时，耗油量最低？最低是多少．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线AB∥CD,将一块三角板EFG如图1所示,△EFG的边与直线AB、CD分别相交于M,N两点，∠F=90°，∠E=30°.
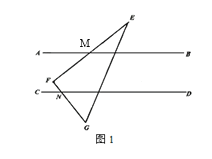
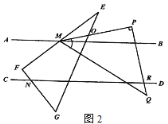
(1)求证:∠EMB+∠DNG=90°
(2)将另一块三角板MPQ如图2放置,△MPQ的边PQ、PM分别与直线CD相交于点R,与△EFG的EG相交于点O,∠P=90°,∠PMQ=45°,直接写出∠PMB与∠PRD的数量关系:
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC和△DEF的顶点A与D重合，已知∠B=90°，∠BAC=30°，BC=6，∠FDE=90°，DF=DE=4．
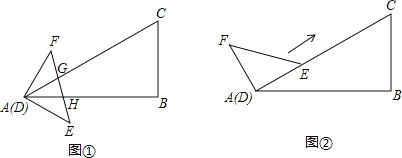
（1）如图①，EF与边AC、AB分别交于点G、H，且FG=EH.设
，在射线DF上取一点P，记： 
，联结CP设△DPC的面积为y，求y关于x的函数解析式，并写出定义域；
（2）在（1）的条件下，求当x为何值时PC//AB；
（3）如图②，先将△DEF绕点D逆时针旋转，使点E恰好落在AC边上，在保持DE边与AC边完全重合的条件下，使△DEF沿着AC方向移动
当△DEF移动到什么位置时，以线段AD、FC、BC的长度为边长的三角形是直角三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．
（1）△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是 ；
（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是 ；（画出图形）
（3）△A2B2C2的面积是 平方单位．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
