
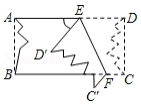
 如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D、C两点分别落在D′、C′的位置,并利用量角器量得∠EFB=66°,则∠AED′等于48度.
如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D、C两点分别落在D′、C′的位置,并利用量角器量得∠EFB=66°,则∠AED′等于48度.  新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:选择题
| A. | 38.4×104 | B. | 3.84×105 | C. | 3.84×106 | D. | 3.84×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上,将△ABC向左平移2格,再向上平移4格.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上,将△ABC向左平移2格,再向上平移4格.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
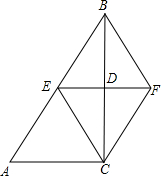 如图在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,请你添加一个条件AC=BC,使四边形BECF是正方形.
如图在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,请你添加一个条件AC=BC,使四边形BECF是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,1 | B. | 5,1 | C. | 2,3 | D. | 2,4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
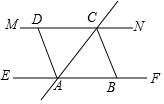 已知EF∥MN,直线AC交EF、MN于点A、C,作∠ACN的角平分线于点B,作∠CAE的角平分线交MN于点D.
已知EF∥MN,直线AC交EF、MN于点A、C,作∠ACN的角平分线于点B,作∠CAE的角平分线交MN于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com