
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНx2+ЃЈ2mЉ1ЃЉxЉ2mЃЈmЃО0.5ЃЉЕФзюЕЭЕуЕФзнзјБъЮЊЉ4ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
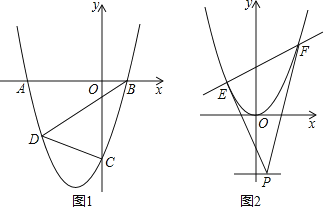
ЃЈ2ЃЉШчЭМ1ЃЌХзЮяЯпгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌDЮЊХзЮяЯпЩЯЕФвЛЕуЃЌBDЦНЗжЫФБпаЮABCDЕФУцЛ§ЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЦНвЦХзЮяЯпyЃНx2+ЃЈ2mЉ1ЃЉxЉ2mЃЌЪЙЦфЖЅЕуЮЊзјБъдЕуЃЌжБЯпyЃНЉ2ЩЯгавЛЖЏЕуPЃЌЙ§ЕуPзїСНЬѕжБЯпЃЌЗжБ№гыХзЮяЯпгаЮЈвЛЕФЙЋЙВЕуEЁЂFЃЈжБЯпPEЁЂPFВЛгыyжсЦНааЃЉЃЌЧѓжЄЃКжБЯпEFКуЙ§ФГвЛЖЈЕуЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНx2+2xЉ3ЃЛЃЈ2ЃЉDЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛЃЈ3ЃЉМћНтЮі
ЃЉЃЛЃЈ3ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЖЅЕузјБъЃЌгЩзюЕЭЕуЕФзнзјБъЮЊЉ4ЃЌПЩСаЗНГЬЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉСЌACНЛBDгкEЃЌЙ§AзїAMЁЭBDгкMЃЌЙ§CзїCNЁЭBDгкNЃЌгЩШ§НЧаЮУцЛ§ЙиЯЕКЭШЋЕШШ§НЧаЮЕФаджЪПЩЧѓЕуEзјБъЃЌПЩЧѓBDНтЮіЪНЃЌМДПЩЧѓЕуDзјБъЃЛ
ЃЈ3ЃЉЩшEЃЈtЃЌt2ЃЉЃЌFЃЈnЃЌn2ЃЉЃЌПЩЧѓPEНтЮіЪНЃЌгЩгыХзЮяЯпгаЮЈвЛЕФЙЋЙВЕуЃЌПЩЧѓk1ЃН2tЃЌМДПЩЧѓЕуPКсзјБъЃЌПЩЕУtnЃНЉ2ЃЌЩшжБЯпEFЕФНтЮіЪНЮЊyЃНkx+bЃЌЕУx2ЉkxЉbЃН0ЃЌПЩЧѓbЃН2ЃЌМДПЩЕУжБЯпEFКуЙ§ЖЈЕуЃЈ0ЃЌ2ЃЉЃЎ
НтЃКЃЈ1ЃЉЁпyЃНx2+ЃЈ2mЉ1ЃЉxЉ2mЃНЃЈx+mЉ0.5ЃЉ2Љm2ЉmЉ0.25ЃЌ
ЁрЖЅЕузјБъЮЊЃЈ0.5ЉmЃЌЉm2ЉmЉ0.25ЃЉ
ЁпзюЕЭЕуЕФзнзјБъЮЊЉ4ЃЌ
ЁрЉm2ЉmЉ0.25ЃНЉ4ЃЌМД4m2+4mЉ15ЃН0ЃЌ
ЁрmЃН1.5ЛђЉ2.5ЃЌ
ЁпmЃО0.5ЃЌЁрmЃН1.5ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНx2+2xЉ3ЃЛ
ЃЈ2ЃЉЁпyЃНx2+2xЉ3гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌ
ЁрAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЎ
ШчЭМЃЌСЌACНЛBDгкEЃЌЙ§AзїAMЁЭBDгкMЃЌЙ§CзїCNЁЭBDгкNЃЌ

ЁпBDЦНЗжЫФБпаЮABCDЕФУцЛ§ЃЌ
ЁрSЁїABDЃНSЁїCBDЃЌ
Ёр![]() BDЁСAMЃН
BDЁСAMЃН![]() BDЁСCNЃЌ
BDЁСCNЃЌ
ЁрAMЃНCNЃЌЧвЁЯAEMЃНЁЯCMNЃЌЁЯAMEЃНЁЯCNEЃН90Ёу
ЁрЁїAEMЁеЁїCENЃЈAASЃЉЃЌ
ЁрAEЃНCEЃЌ
ЁрEЃЈЉ1.5ЃЌЉ1.5ЃЉЃЌЧвBЃЈ1ЃЌ0ЃЉЃЌ
ЁржБЯпBEЕФНтЮіЪНЮЊyЃН0.6xЉ0.6ЃЎ
Ёр0.6xЉ0.6ЃНx2+2xЉ3ЃЌ
НтЕУx1ЃНЉ![]() ЃЌx2ЃН1ЃЌ
ЃЌx2ЃН1ЃЌ
ЁрDЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉгЩЬтвтПЩЕУЦНвЦКѓНтЮіЪНЮЊyЃНx2ЃЌ
ЩшEЃЈtЃЌt2ЃЉЃЌFЃЈnЃЌn2ЃЉЃЌ
ЩшжБЯпPEЮЊyЃНk1ЃЈxЉtЃЉ+t2ЃЌ
гЩЬтвтПЩЕУ x2Љk1x+k1tЉt2ЃН0ЃЌ
ЁрЁїЃНk12Љ4ЃЈk1tЉt2ЃЉЃНЃЈk1Љ2tЃЉ2ЃН0ЃЌ
Ёрk1ЃН2tЃЎ
ЁржБЯпPEЮЊyЃН2tЃЈxЉtЃЉ+t2ЃЌМДyЃН2txЉt2ЃЎ
СюyЃНЉ2ЃЌЕУxPЃН![]() ЃЌ
ЃЌ
ЭЌРэЃЌЩшжБЯпPFЮЊyЃНk2ЃЈxЉnЃЉ+n2ЃЌ
ЁрxPЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпtЁйnЃЌ
ЁрtnЃНЉ2ЃЎ
ЩшжБЯпEFЕФНтЮіЪНЮЊyЃНkx+bЃЌЕУx2ЉkxЉbЃН0ЃЌ
ЁрxExFЃНЉbЃЌМДtnЃНЉbЃЌ
ЁрbЃН2ЃЎ
ЁржБЯпEFЮЊyЃНkx+2ЃЌЙ§ЖЈЕуЃЈ0ЃЌ2ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCдкЦНУцжБНЧзјБъЯЕжаЃЌЁЯACBЃН90ЁуЃЌACЃНBCЃЌAЕФзјБъЪЧЃЈ0ЃЌmЃЉЃЈmЃМ0ЃЉЃЌЕуCЕФзјБъЪЧЃЈ2ЃЌ0ЃЉЃЌЕуBдкxжсЩЯЗНЃЎ
ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌШєЕуBдкyжсЩЯЃЌдђmЕФжЕЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃЌBCгыyжсНЛгкЕуDЃЎ
ЂйШєmЃНЉ6ЃЌЧѓЕуBЕФзјБъЃЛ
ЂкШєyжсЧЁКУЦНЗжЁЯBACЃЌЧѓODЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
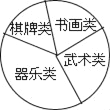
ЁОЬтФПЁПФГаЃбЇЩњЛсзМБИЕїВщСљФъМЖбЇЩњВЮМгЁАЮфЪѕРрЁБЁЂЁАЪщЛРрЁБЁЂЁАЦхХЦРрЁБЁЂЁАЦїРжРрЁБЫФРраЃБОПЮГЬЕФШЫЪ§ЃЎ
ЃЈ1ЃЉШЗЖЈЕїВщЗНЪНЪБЃЌМзЭЌбЇЫЕЃКЁАЮвЕНСљФъМЖЃЈ1ЃЉАрШЅЕїВщШЋЬхЭЌбЇЁБЃЛввЭЌбЇЫЕЃКЁАЗХбЇЪБЮвЕНаЃУХПкЫцЛњЕїВщВПЗжЭЌбЇЁБЃЛБћЭЌбЇЫЕЃКЁАЮвЕНСљФъМЖУПИіАрЫцЛњЕїВщвЛЖЈЪ§СПЕФЭЌбЇЁБЃЎЧыжИГіФФЮЛЭЌбЇЕФЕїВщЗНЪНзюКЯРэЃЎ
РрБ№ | ЦЕЪ§ЃЈШЫЪ§ЃЉ | ЦЕТЪ |
ЮфЪѕРр | 0.25 | |
ЪщЛРр | 20 | 0.20 |
ЦхХЦРр | 15 | b |
ЦїРжРр | ||
КЯМЦ | a | 1.00 |
ЃЈ2ЃЉЫћУЧВЩгУСЫзюЮЊКЯРэЕФЕїВщЗНЗЈЪеМЏЪ§ОнЃЌВЂЛцжЦСЫШчЭМЫљЪОЕФЭГМЦБэКЭЩШаЮЭГМЦЭМЃЎ
ЧыФуИљОнвдЩЯЭМБэЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
Ђйa=_____ЃЌb=_____ЃЛ
ЂкдкЩШаЮЭГМЦЭМжаЃЌЦїРжРрЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ_____ЃЛ
ЂлШєИУаЃСљФъМЖгабЇЩњ560ШЫЃЌЧыФуЙРМЦДѓдМгаЖрЩйбЇЩњВЮМгЮфЪѕРраЃБОПЮГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
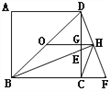
ЁОЬтФПЁПШчЭМЃЌЕуOЮЊе§ЗНаЮABCDЕФжааФЃЌBEЦНЗжЁЯDBCНЛDCгкЕуEЃЌбгГЄBCЕНЕуFЃЌЪЙFC=ECЃЌСЌНсDFНЛBEЕФбгГЄЯпгкЕуHЃЌСЌНсOHНЛDCгкЕуGЃЌСЌНсHC.дђвдЯТЫФИіНсТлжаЃКЂйOHЁЮBFЃЌЂкGH=![]() BC,ЂлOD=
BC,ЂлOD=![]() BF,ЂмЁЯCHF=45ЁуЁЃе§ШЗНсТлЕФИіЪ§ЮЊ( )
BF,ЂмЁЯCHF=45ЁуЁЃе§ШЗНсТлЕФИіЪ§ЮЊ( )
A. 4Иі B. 3Иі C. 2Иі D. 1Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФЯЖДЭЅДѓЧХЪЧФЯвцИпЫйЙЋТЗЩЯЕФживЊЧХСКЃЌаЁЗМЭЌбЇдкаЃЭтЪЕМљЛюЖЏжаЖдДЫПЊеЙВтСПЛюЖЏЃЎШчЭМЃЌдкЧХЭтвЛЕуAВтЕУДѓЧХжїМмгыЫЎУцЕФНЛЛуЕуCЕФИЉНЧЮЊІСЃЌДѓЧХжїМмЕФЖЅЖЫDЕФбіНЧЮЊІТЃЌвбжЊВтСПЕугыДѓЧХжїМмЕФЫЎЦНОрРыABЃНaЃЌдђДЫЪБДѓЧХжїМмЖЅЖЫРыЫЎУцЕФИпCDЮЊ( )
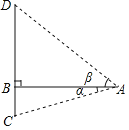
A.asinІС+asinІТB.acosІС+acosІТC.atanІС+atanІТD.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуBдкКЏЪ§yЃНxЭМЯѓЩЯЃЌЕуAдкxжсЕФе§АыжсЩЯЃЌЕШбќжБНЧШ§НЧаЮBCDЕФЖЅЕуCдкABЩЯЃЌЕуDдкКЏЪ§yЃН![]() ЕквЛЯѓЯоЕФЭМЯѓЩЯШєЁїOABгыЁїBCDУцЛ§ЕФВюЮЊ2ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЕквЛЯѓЯоЕФЭМЯѓЩЯШєЁїOABгыЁїBCDУцЛ§ЕФВюЮЊ2ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
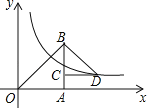
A.8B.4C.2D.1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬНОПЃКШчЭМЂйЃЌжБЯпl1ЁЮl2ЃЌЕуAЁЂBдкжБЯпl1ЩЯЃЌЕуCЁЂDдкжБЯпl2ЩЯЃЌМЧЁїABCЕФУцЛ§ЮЊS1ЃЌЁїABDЕФУцЛ§ЮЊS2ЃЌЧѓжЄЃКS1ЃНS2ЃЎ
ЭиеЙЃКШчЭМЂкЃЌEЮЊЯпЖЮABбгГЄЯпЩЯвЛЕуЃЌBEЃОABЃЌе§ЗНаЮABCDЁЂе§ЗНаЮBEFGОљдкжБЯпABЭЌВрЃЌЧѓжЄЃКЁїDEGЕФУцЛ§ЪЧе§ЗНаЮBEFGУцЛ§ЕФвЛАыЃЎ
гІгУЃКШчЭМЂлЃЌдквЛЬѕжБЯпЩЯвРДЮгаЕуAЁЂBЁЂCЁЂDЃЌе§ЗНаЮABIJЁЂе§ЗНаЮBCGHЁЂе§ЗНаЮCDEFОљдкжБЯпABЭЌВрЃЌЧвЕуFЁЂHЗжБ№ЪЧБпCGЁЂBIЕФжаЕуЃЌШєе§ЗНаЮCDEFЕФУцЛ§ЮЊlЃЌдђЁїAGIЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
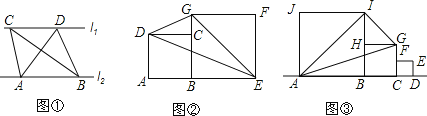
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
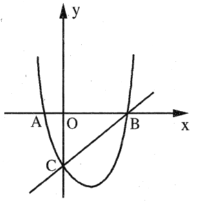
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§ЕФЭМЯѓНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЯТЗНХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЯТЗНХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪН;
ЃЈ2ЃЉСЌНг![]() ЃЌЪЧЗёДцдкЕу
ЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() УцЛ§зюДѓЃЌШєДцдкЃЌЧѓГіЕу
УцЛ§зюДѓЃЌШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌBCЃНkACЃЌЕуDдкACЩЯЃЌСЌНгBDЃЎ
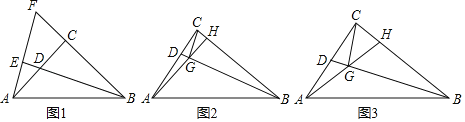
ЃЈ1ЃЉШчЭМ1ЃЌЕБkЃН1ЪБЃЌBDЕФбгГЄЯпДЙжБгкAEЃЌДЙзуЮЊEЃЌбгГЄBCЁЂAEНЛгкЕуFЃЎЧѓжЄЃКCDЃНCFЃЛ
ЃЈ2ЃЉЙ§ЕуCзїCGЁЭBDЃЌДЙзуЮЊGЃЌСЌНгAGВЂбгГЄНЛBCгкЕуHЃЎ
ЂйШчЭМ2ЃЌШєCHЃН![]() CDЃЌЬНОПЯпЖЮAGгыGHЕФЪ§СПЙиЯЕЃЈгУКЌkЕФДњЪ§ЪНБэЪОЃЉЃЌВЂжЄУїЃЛ
CDЃЌЬНОПЯпЖЮAGгыGHЕФЪ§СПЙиЯЕЃЈгУКЌkЕФДњЪ§ЪНБэЪОЃЉЃЌВЂжЄУїЃЛ
ЂкШчЭМ3ЃЌШєЕуDЪЧACЕФжаЕуЃЌжБНгаДГіcosЁЯCGHЕФжЕЃЈгУКЌkЕФДњЪ§ЪНБэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com