
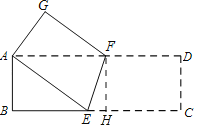
【题目】如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕.若AB=3,BC=9.点D对应点是G.

(1)求BE长;
(2)求EF长.
【答案】(1)4;(2)![]()
【解析】
(1)由翻折可知:AE=EC,设AE=EC=x,则BE=9﹣x,在Rt△ABE中,利用勾股定理构建方程即可解决问题.
(2)作FH⊥BC于H,则四边形ABHF是矩形,求出FH,EH,利用勾股定理即可解决问题.
解:(1)∵四边形ABCD是矩形,
∴∠B=90°,
由翻折可知:AE=EC,设AE=EC=x,则BE=9﹣x,
在Rt△ABE中,∵AB2+BE2=AE2,
∴32+(9﹣x)2=x2,
∴x=5,
∴BE=9﹣5=4.
(2)作FH⊥BC于H,则四边形ABHF是矩形,
∴FH=AB=3,
∵AD∥BC,
∴∠AFE=∠FEC,
∵∠FEC=∠FEA,
∴∠AFE=∠FEA,
∴AF=AE=BH=5,
∴EH=BH﹣BE=1,
∴EF=![]() =
=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

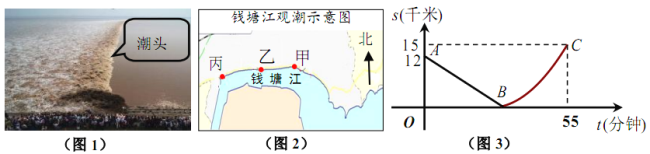
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离![]() (千米)与时间
(千米)与时间![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点![]() ,点
,点![]() 坐标为
坐标为![]() ,曲线
,曲线![]() 可用二次函数
可用二次函数![]() (
(![]() ,
,![]() 是常数)刻画.
是常数)刻画.
(1)求![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度![]() ,
,![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,顶点在格点上的三角形叫做格点三角形,如格点三角形△ABC.

(1)△ABC的面积为 ;
(2)△ABC的形状为 ;
(3)根据图中标示的各点(A、B、C、D、E、F)位置,与△ABC全等的格点三角形是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
因式分解:![]() .
.
解:将“![]() ”看成整体,令
”看成整体,令![]() ,则原式
,则原式![]() .
.
再将“![]() ”还原,原式
”还原,原式![]() .
.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
(问题解决)
(1)因式分解:![]() ;
;
(2)因式分解:![]() ;
;
(3)证明:若![]() 为正整数,则代数式
为正整数,则代数式![]() 的值一定是某个整数的平方.
的值一定是某个整数的平方.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com