
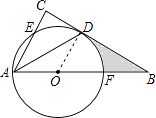
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F. (Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2 ![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).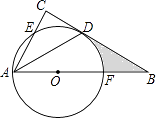
【答案】解:(Ⅰ)BC与⊙O相切. 证明:连接OD.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∵OD=OA,
∴∠OAD=∠ODA.
∴∠CAD=∠ODA.
∴OD∥AC.
∴∠ODB=∠C=90°,即OD⊥BC.
又∵BC过半径OD的外端点D,
∴BC与⊙O相切.
(Ⅱ)设OF=OD=x,则OB=OF+BF=x+2,
根据勾股定理得:OB2=OD2+BD2 , 即(x+2)2=x2+12,
解得:x=2,即OD=OF=2,
∴OB=2+2=4,
∵Rt△ODB中,OD= ![]() OB,
OB,
∴∠B=30°,
∴∠DOB=60°,
∴S扇形AOB= ![]() =
= ![]() ,
,
则阴影部分的面积为S△ODB﹣S扇形DOF= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]() =2
=2 ![]() ﹣
﹣ ![]() .
.
故阴影部分的面积为2 ![]() ﹣
﹣ ![]() .
.
【解析】(Ⅰ)连接OD,证明OD∥AC,即可证得∠ODB=90°,从而证得BC是圆的切线; (Ⅱ)在直角三角形OBD中,设OF=OD=x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为圆的半径,求出圆心角的度数,直角三角形ODB的面积减去扇形DOF面积即可确定出阴影部分面积.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,由于各人的习惯不同,双手交叉时左手大拇指在上或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如表所示:
2011届 | 2012届 | 2013届 | 2014届 | 2015届 | |
参与实验的人数 | 106 | 110 | 98 | 104 | 112 |
右手大拇指在上的人数 | 54 | 57 | 49 | 51 | 56 |
频率 | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F. 
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( ) ①两等分 ②三等分 ③四等分 ④五等分.
A.②
B.①②
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求:
(1)∠FED的度数;
(2)∠FEG的度数;
(3)∠1和∠2的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O. 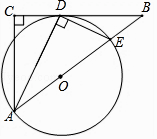
(1)求证:BC是⊙O的切线;
(2)若AC=3,BC=4,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com