
分析 可以分别从若BC是底边,即AB=AC与若BC是腰BC=BA,①点D在BC边上,②若点D在CB的延长线上去分析,根据等腰三角形的性质与直角三角形的性质,即可求得答案.
解答 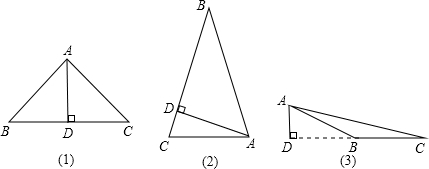 解:∵AD是BC边上的高线,
解:∵AD是BC边上的高线,
若BC是底边,即AB=AC,如图(1)所示,
∴BD=DC,AD⊥BC,∠BAD=∠CAD
∵AD=BD
∴∠B=∠BAD=45°
∴∠BAC=2∠BAD=90°
若BC是腰BC=BA,
①若点D在BC边上,如图(2)所示,
则在Rt△BAD中,
∵BA=2AD,
∴∠B=30°,
∴∠BAC=75°;
②若点D在CB的延长线上,如图(3)所示,
类似地,得:∠DBA=30°,
则:∠ABC=150°,
∴∠BAC=15°.
综上:∠BAC的度数为90°,75°,15°.
点评 此题主要考查等腰三角形三线合一的性质,以及直角三角形的性质,关键是掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.注意分类讨论思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
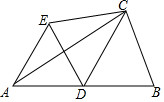 如图,在△ABC中,CD是AB边的中线,∠CDB=60°,将△BCD沿CD折叠,使点B落在点E的位置.
如图,在△ABC中,CD是AB边的中线,∠CDB=60°,将△BCD沿CD折叠,使点B落在点E的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
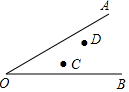 如图所示,在V形公路(即∠AOB)内部有两个村庄C、D,你能选择一个纺织厂的厂址P,使P到V形公路的两条路的距离相等,且使C、D两村庄的工人上下班的路程一样吗?
如图所示,在V形公路(即∠AOB)内部有两个村庄C、D,你能选择一个纺织厂的厂址P,使P到V形公路的两条路的距离相等,且使C、D两村庄的工人上下班的路程一样吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com