
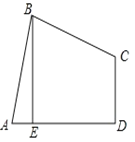
【题目】如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE=( )
A.2B.3C.4D.5
【答案】C
【解析】
作BF⊥CD交CD的延长线于点F,根据直角三角形两锐角互余的关系可得∠ABE=∠CBF,利用AAS可证明△ABE≌△CBF,可得BE=BF;四边形ABCD的面积等于新正方形FBED的面积,根据∠BED=∠CDE=∠BFC=90°,可证明四边形BEDF是正方形,即可得BE=3.
过B作BF垂直DC的延长线于点F,
∵∠ABC=∠CDA=90°,BF⊥DF,
∴∠ABE+∠EBC=∠CBF+∠EBC,
∴∠ABE=∠CBF;
又∵BE⊥AD,BF⊥DF,且AB=BC,
∴△ABE≌△CBF,
∴BE=BF;四边形ABCD的面积等于四边形BEDF的面积
∵BE⊥AD,∠CDA=90°,DF⊥DF,
∴四边形BEDF是矩形,
又∵BE=BF,
∴四边形BEDF为正方形;
∵四边形ABCD的面积为16,
∴正方形BEDF的面积为16,
∴BE=4

故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
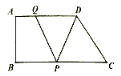
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 以每秒2个单位长的速度运动,动点
以每秒2个单位长的速度运动,动点![]() 同时从点
同时从点![]() 出发,在边
出发,在边![]() 上以每秒1个单位长的速度向点
上以每秒1个单位长的速度向点![]() 运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为
运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为![]() (秒),
(秒),
(1)①设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 为何值时,
为何值时,![]() ?
?![]() 能不能等于
能不能等于![]() ?为什么?
?为什么?
(2)①当![]() 为何值时,
为何值时,![]() ?
?
②当![]() 为何值时,点
为何值时,点![]() 是在
是在![]() 的垂直平分线上?
的垂直平分线上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型衬衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)求甲、乙两种款型的衬衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型剩余的按标价的五折降价销售,很快全部售完。求售完这批衬衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,运动到3秒钟时,两点相距15个单位长度.已知动点A、B的运动速度比之是3:2(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)A、B两点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
(3)若A、B两点分别从(2)中标出的位置再次同时开始在数轴上运动,运动的速度不变,运动的方向不限,问:经过几秒钟,A、B两点之间相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2020年元月的日历表中,某一天对应的号数的上、下、左、右四个数的和为![]() .
.
(1)如果某一天是![]() 号,请用含
号,请用含 ![]() 的代数式把
的代数式把![]() 表示出来;
表示出来;
(2)![]() 的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
(3)![]() 的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com