
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作ABDE,连接AD、EC. 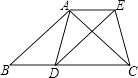
(1)试说明:△ADC≌△ECD;
(2)若BD=CD,试说明:四边形ADCE是矩形.
【答案】
(1)证明:∵AB=AC,
∴∠B=∠ACB,
又∵ABDE中,AB=DE,AB∥DE,
∴∠B=∠EDC=∠ACB,AC=DE,
在△ADC和△ECD中,
 ,
,
∴△ADC≌△ECD(SAS).
(2)解:∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,
∵D为边长中点,
∴BD=CD,
∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵△ADC≌△ECD,
∴AC=DE,
∴四边形ADCE是矩形.
【解析】(1)利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB,则易证△ADC≌△ECD,利用全等三角形的对应边相等即可证得;(2)根据平行四边形性质推出AE=BD=CD,AE∥CD,得出平行四边形,根据AC=DE推出即可.
【考点精析】利用平行四边形的性质和矩形的判定方法对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


科目:初中数学 来源: 题型:
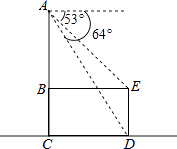
【题目】如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?
(参考数据:tan53°≈ ![]() ,sin53°≈
,sin53°≈ ![]() ,tan64°≈2,sin64°≈
,tan64°≈2,sin64°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若∠BAC=90°,AC平分∠EAF,且BC=8cm,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
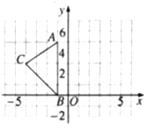
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);
⑵直接写出A’,B’,C’三点的坐标:A’ ( ),B’( ),C’( );
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,某学习小组对有一内角(∠BAD)为120°的平行四边形ABCD,将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究:在(2)的条件下,学习小组某成员探究发现AE+2AF= ![]() AC,试判断结论是否正确,并说明理由.
AC,试判断结论是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)求证:EG=FG.
(2)若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为 . 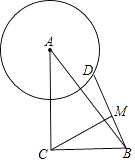
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快走是大众常用的健身方式,手机中的“乐动力”可以计算行走的步数与消耗的相应能量,对比数据发现小明步行1200步与小红步行9000步消耗的能量相同,若每消耗1千卡能量小明行走的步数比小红多2步,求小红每消耗1千卡能量可以行走多少步?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com