
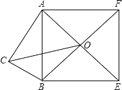
【题目】如图,在Rt△ABC中,∠C=90°,AC=5,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,![]() ,则BC边的长为_.
,则BC边的长为_.
【答案】3
【解析】
作EQ⊥x轴,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,5).设B(x,0),由于O点为以AB一边向三角形外作正方形ABEF的中心,利用AAS得到三角形ABC与三角形BEQ全等,利用全等三角形的对应边相等得到AC=BQ=5,BC=EQ,设BC=EQ=x,由OM为梯形ACQE的中位线,利用梯形中位线定理表示出OM,再由CM,表示出O坐标,进而表示出OC的长,根据已知OC的长列出关于x的方程,求出方程的解得到x的值,即可确定出BC的长.
解:作EQ⊥x轴,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,5).
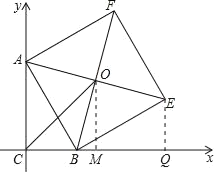
设B(x,0),由于O点为以AB一边向三角形外作正方形ABEF的中心,
∴AB=BE,∠ABE=90°,
∵∠ACB=90°,
∴∠BAC+∠ABC=90°,∠ABC+∠EBQ=90°,
∴∠BAC=∠EBQ,
在△ABC和△BEQ中,
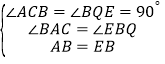 ,
,
∴△ACB≌△BQE(AAS),
∴AC=BQ=5,BC=EQ,
设BC=EQ=x,
∴O为AE中点,
∴OM为梯形ACQE的中位线,
∴OM=![]() ,
,
又∵CM=![]() CQ=
CQ=![]() ,
,
∴O点坐标为(![]() ,
,![]() ),
),
根据题意得:OC=4![]() =
=![]() ,
,
解得:x=3,
则BC=3.
故答案为:3.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】某校初级中学初一、初二、初三三个年段均有学生500人,为了解数学史知识的普及情况,按年段以2%的比例随机抽样,然后进行模拟测试,测试成绩整理如下:
初一年段 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
初二年段 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
初三年段 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从样本成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求各年段恰好都有一名学生参加的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
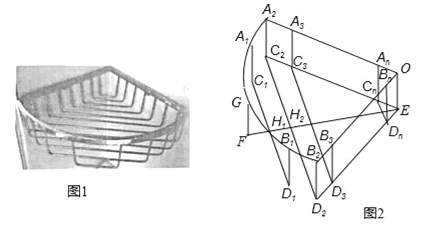
【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在![]() 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .一动点
.一动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 匀速运动,到达
匀速运动,到达![]() 点后,立即以原速度沿
点后,立即以原速度沿![]() 返回;另一动点
返回;另一动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 匀速运动,点
匀速运动,点![]() 、
、![]() 同时出发,当两点相遇时停止运动.在点
同时出发,当两点相遇时停止运动.在点![]() 、
、![]() 的运动过程中,以
的运动过程中,以![]() 为边作等边
为边作等边![]() ,使
,使![]() 和矩形
和矩形![]() 在射线
在射线![]() 的同侧,设运动的时间为
的同侧,设运动的时间为![]() 秒(
秒(![]() ).
).

(1)当等边![]() 的边
的边![]() 恰好经过点
恰好经过点![]() 时,求运动时间
时,求运动时间![]() 的值;
的值;
(2)在![]() 未到达
未到达![]() 的过程中,设等边
的过程中,设等边![]() 和矩形
和矩形![]() 重叠部分的面积为
重叠部分的面积为![]() ,请求出
,请求出![]() 与
与![]() 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
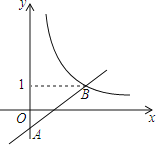
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(t,1).
(x>0)的图象相交于点B(t,1).
(1)求点B的坐标及一次函数的解析式;
(2)点P的坐标为(m,m)(m>0),过P作PE∥x轴,交直线AB于点E,作PF∥y轴,交函数![]() (x>0)的图象于点F.
(x>0)的图象于点F.
①若m=2,比较线段PE,PF的大小;
②直接写出使PE≤PF的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
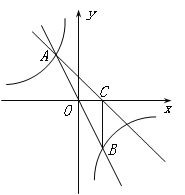
(1)求m、n的值;
(2)求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
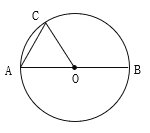
【题目】如图,在⊙O中,AB是直径,半径为R,弧AC=![]() R.
R.
求:(1)∠AOC的度数.(2)若D为劣弧BC上的一动点,且弦AD与半径OC交于E点.试探求△AEC≌△DEO时,D点的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com