
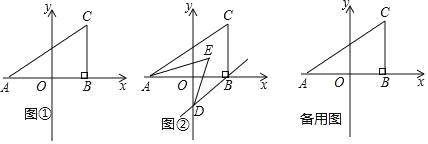
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
【答案】(1)4;(2)∠AED=45°;(3)P(0,-1)或(0,3).
【解析】
(1)先依据非负数的性质可求得a、b的值,从而可得到点A、点B和点C的坐标,接下来,依据三角形的面积公式求解即可;
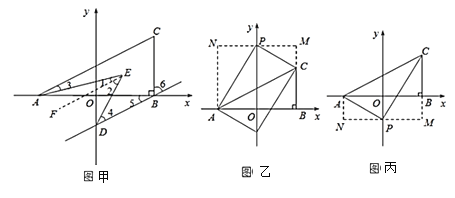
(2)如图甲所示:过E作EF∥AC.首先依据平行线的性质可知∠ODB=∠6,∠CAB=∠5,接下来,依据平行公理的推理可得到BD∥AC∥EF,然后,依据平行线的性质可得到∠1=∠3,∠2=∠4,然后,依据角平分线的性质可得到∠3=![]() ∠CAB,∠4=
∠CAB,∠4=![]() ∠ODB,最后,依据∠AED=∠1+∠2=∠3+∠4求解即可;
∠ODB,最后,依据∠AED=∠1+∠2=∠3+∠4求解即可;
(3)①当P在y轴正半轴上时,设点P(0,t),分别过点P,A,B作MN∥x轴,AN∥y轴,BM∥y轴,交于点M,N,然后,用含t的式子表示出AN,CM的长,然后依据S三角形ACP=S梯形MNAC-S三角形ANP-S三角形CMP列出关于t的方程求解即可;②当P在y轴负半轴上时,如图丙分别过点P,A,B作MN∥x轴,AN∥y轴,BM∥y轴,交于点M,N,设点P(0,t),然后用含t的式子表示出AN、CM的长,最后,依据S三角形ACP=S梯形MNAC-S三角形ANP-S三角形CMP列方程求解即可.
解:(1)∵(a+2)2+![]() =0,
=0,
∴a+2=0,b-2=0,
∴a=-2,b=2,
∵CB⊥AB,
∴A(-2,0),B(2,0),C(2,2),
∴△ABC的面积=![]() ×2×4=4;
×2×4=4;
(2)∵CB//y轴,BD//AC,
∴∠CAB=∠5,∠ODB=∠6,∠CAB+∠ODB=∠5+∠6=90°,
过E作EF//AC,如图①
∵BD//AC,
∴BD//AC//EF,
∵AE、DE分别平分∠CAB、∠ODB,
∴∠3=![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4=![]() ∠ODB=∠2,
∠ODB=∠2,
∴∠AED=∠1+∠2=![]() (∠CAB+∠ODB)=45°
(∠CAB+∠ODB)=45°
(3)①当P在y轴正半轴上时,如图②,
设P(0,t),过P作MN//x轴,AN//y轴,BM//y轴,
∵S△APC=S梯形MNAC-S△CMP-S△ANP=4,
∴![]() -t-(t-2)=4,
-t-(t-2)=4,
解得:t=3,
②当P在y轴负半轴上时,如图③,设P(0,t),过P作MN//x轴,AN//y轴,BM//y轴,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4,
∴![]() +t-(2-t)=4,
+t-(2-t)=4,
解得:t= -1,
∴P(0,-1)或(0,3).
故答案为(1)4;(2)∠AED=45°;(3)P(0,-1)或(0,3).


科目:初中数学 来源: 题型:
【题目】寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(3,0)两点,点C是抛物线与y轴的交点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)在抛物线的对称轴上是否存在点M,使△BCM是等腰三角形,若存在请直接写出点M坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).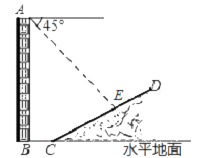
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国的固有领土,现在我南海渔民要在南沙群岛某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+ ![]() )海里的C处,为防止某国的巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
)海里的C处,为防止某国的巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.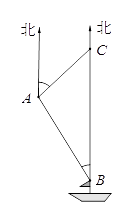
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.
(1)当t= s时,以OB、OP为邻边的平行四边形是菱形;
(2)当点P在OB的垂直平分线上时,求t的值;
(3)将△OBP沿直线OP翻折,使点B的对应点D恰好落在x轴上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,当x=1时,y=1;当x=-2时,y=-14.
(1)求这个一次函数的关系式;
(2)在如图所示的平面直角坐标系中作出函数的图像;
(3)由图像观察,当0≤x≤2时,函数y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com