

分析 分三段考虑,①点P在AB上,②点P在BC上,分别用含t的式子表示出△BPD的面积,再由S=3cm2建立方程,解出t的值即可.
解答 解:①当点P在AB上时,点P的速度为1cm/s,0<t<3,如图①所示: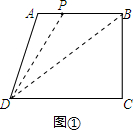 ,
,
则BP=AB-AP=3-t,
S△BPD=$\frac{1}{2}$BP×CB=$\frac{9}{2}$-$\frac{3t}{2}$=3,
解得:t=1.
②当点P在BC上时,点P的速度为1cm/s,3<t≤6,如图②所示: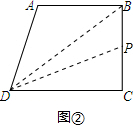 ,
,
则BP=t-3,
S△BPD=$\frac{1}{2}$BP×DC=2t-6=3,
解得:t=4.5.
综上可得:当t=1秒或4.5秒时,使得△BPD的面积S=3cm2
点评 本题考查了梯形的知识,解答本题的关键是分段讨论,画出每段的图形,根据△BPD的面积为3建立方程,注意数形结合思想的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com