
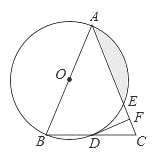
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
【答案】(1)见解析;(2)4π﹣8.
【解析】试题分析:(1)连接OD,易得∠ABC=∠ODB,由AB=AC,易得∠ABC=∠ACB,等量代换得∠ODB=∠ACB,利用平行线的判定得OD∥AC,由切线的性质得DF⊥OD,得出结论;
(2)连接OE,利用(1)的结论得∠ABC=∠ACB=67.5°,易得∠BAC=45°,得出∠AOE=90°,利用扇形的面积公式和三角形的面积公式得出结论.
试题解析:(1)连接OD,
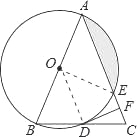
∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC,
∵DF是⊙O的切线,
∴DF⊥OD,
∴DF⊥AC.
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE="8" ,
∴S阴影=4π-8.


科目:初中数学 来源: 题型:
【题目】若整数a能被整数b整除,则一定存在整数n,使得![]() =n,即a=bn,例如:若整数a能被整数7整除,则一定存在整数n,使得
=n,即a=bn,例如:若整数a能被整数7整除,则一定存在整数n,使得![]() =n,即a=7n.
=n,即a=7n.
(1)将一个多位自然数分解为个位与个位之前的数,让个位之前的数减去个位数的两倍,若所得之差能被7整除,则原多位自然数一定能被7整除.例如:将数字1078分解为8和107,107﹣8×2=91,因为91能被7整除,所以1078能被7整除,请你证明任意一个三位数都满足上述规律.
(2)若将一个多位自然数分解为个位与个位之前的数,让个位之前的数加上个位数的k(k为正整数,1≤k≤15)倍,所得之和能被13整除,求当k为何值时使得原多位自然数一定能被13整除.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
(1)两条直线不相交就平行
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行
A. 0 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
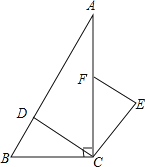
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.同一平面内不相交的两线段必平行
B.同一平面内不相交的两射线必平行
C.同一平面内不相交的一条线段与一条直线必平行
D.同一平面内不相交的两条直线必平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com