
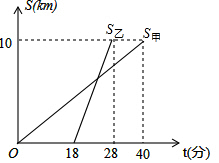
 甲、乙两位教师先后从学校出发,到距学校10千米的培训中心参加新教材培训学习,图中S甲、S乙分别表示甲、乙两位教师从学校到培训中心所走的路程s(千米)随时间t(分钟)变化的函数图象.求乙出发后追上甲所用的时间是多少?
甲、乙两位教师先后从学校出发,到距学校10千米的培训中心参加新教材培训学习,图中S甲、S乙分别表示甲、乙两位教师从学校到培训中心所走的路程s(千米)随时间t(分钟)变化的函数图象.求乙出发后追上甲所用的时间是多少? 分析 根据函数图象可以分别求出甲乙对应的函数解析式,然后令它们的函数值相等即可解答本题.
解答 解:设s甲与t函数关系式为s甲=kt,
40k=10,得k=0.25,
即s甲与t函数关系式为s甲=0.25t,
设s乙与t函数关系式为s乙=at+b,
$\left\{\begin{array}{l}{18a+b=0}\\{28a+b=10}\end{array}\right.$,得$\left\{\begin{array}{l}{a=1}\\{b=-18}\end{array}\right.$,
即s乙与t函数关系式为s乙=t-18,
令0.25t=t-18,
解得,t=24,
∵24-18=6,
∴乙出发6分钟甲乙两人相遇,
答:乙出发后追上甲所用的时间是6分钟.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用一次函数的性质解答.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com