
 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | π | C. | π-$\sqrt{3}$ | D. | $\sqrt{3}$ |
分析 连接DE、OE、OD,可得△OAE、△ODE、△OBD、△CDE都是等边三角形,由此可求出扇形OBE的圆心角的度数和圆的半径长;由于∠AOE=∠BOD,则AB∥DE,S△ODE=S△BDE;根据阴影部分的面积=S扇形OAE-S△OAE+S扇形ODE求解即可.
解答 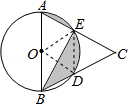 解:连接OE、OD,点D、E是半圆的三等分点,
解:连接OE、OD,点D、E是半圆的三等分点,
∴∠AOE=∠EOD=∠DOB=60°
∵OA=OE=OD=OB
∴△OAE、△ODE、△OBD、△CDE都是等边三角形,
∴AB∥DE,S△ODE=S△BDE;
∴图中阴影部分的面积=S扇形OAE-S△OAE+S扇形ODE=$\frac{60•π×{2}^{2}}{360}$×2-$\frac{\sqrt{3}}{4}$×22=$\frac{4}{3}$π-$\sqrt{3}$.
故选A.
点评 本题考查了扇形面积公式的运用.关键是将阴影部分面积转化为规则图形的面积的和或差.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
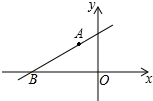 如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.
如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
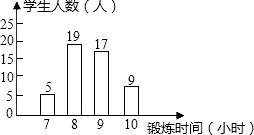 阳光体育运动,要求学生每一天锻炼一小时,如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图,那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时.
阳光体育运动,要求学生每一天锻炼一小时,如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图,那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
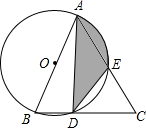 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交于点D、E,连接DE、AD.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交于点D、E,连接DE、AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
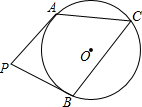 如图,PA,PB分别与⊙O相切于A,B两点,sin∠C=$\frac{4}{5}$,PA=$\frac{20}{3}$,则⊙O的面积为( )
如图,PA,PB分别与⊙O相切于A,B两点,sin∠C=$\frac{4}{5}$,PA=$\frac{20}{3}$,则⊙O的面积为( )| A. | 16π | B. | 25π | C. | 9π | D. | 8π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com