
���ı���ABCD�У���B=90�㣬AC=4��AB��CD��DH��ֱƽ��AC����HΪ���㣮��AB=x��AD=y����y����x�ĺ�����ϵ��ͼ����¿��Ա�ʾΪ��������

A.  B.
B.  C.
C.  D.
D. 

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ���� ������ ���ͣ���ѡ��
��ͼ����·���ڵ����˶̱۳�1m�����۳�16m.���̱۶˵��½�0.5mʱ�����۶˵����ߣ��˵Ŀ��Ⱥ��Բ��ƣ�

A. 4m B. 6m C. 8m D. 12m
C ������������������賤�۶˵�����x�ף����ã�x=8����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݽ���2016-2017ѧ�����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
��ͼ����֪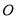 Ϊֱ��
Ϊֱ�� ��һ�㣬
��һ�㣬 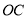 ƽ��
ƽ��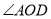 ��
�� 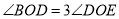 ��
��  ����
����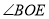 �Ķ���Ϊ_________�����ú�
�Ķ���Ϊ_________�����ú� �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²� ���в��Ծ� ���ͣ������
��ͼ��Rt��ABC�У���ACB=90�㣬AC=6cm��BC=8cm������P�ӵ�B��������BA������ÿ��5cm���ٶ����A�����˶���ͬʱ����Q�ӵ�C��������CB������ÿ��4cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��2��������PQ��

��1������BPQ���ABC���ƣ���t��ֵ��
��2������AQ��CP����AQ��CP����t��ֵ��
(1) t=1�� ;(2) ����������������� ��1���ɡ�B�ǡ�BPQ���ABC�Ĺ����ǣ���֪���������������ƣ���������������١�BPQ�ס�BAC���ڡ�BPQ�ס�BCA�������������������������ε����ʺ����⼴�ɽ�ö�Ӧ��t��ֵ�� ��2����ͼ1����P��PM��BC�ڵ�M��AQ��CP���ڵ�N���������֪����AQ��CPʱ����ACQ�ס�CMP�������������ε������г�����ʽ���ɽ�ö�Ӧ��t...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²� ���в��Ծ� ���ͣ������
��������ֽƬ����ABC������ͼ��ʾ�ķ�ʽ�۵���ʹ��B���ڱ�AC�ϣ���Ϊ��B�䣬�ۺ�ΪEF����֪AB��AC��6��BC��8�����Ե�B�䣬F��CΪ��������������ABC���ƣ���BF�ij�����______

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²� ���в��Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ����������в����жϡ�ABC�ס�AED���ǣ� ��
A����AED=��B B����ADE=��C C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��3�� ��ʽ����Ӽ� ��Ԫ���Ծ� ���ͣ������
������ʽ(4x2��mx��3y��4)��(8nx2��x��2y��3)��ֵ����ĸx��ȡֵ�أ������ʽ(��m2��2mn��n2)��2(mn��3m2)��3(2n2��mn)��ֵ��
. �������������������֪����ʽȥ���źϲ����ݽ����x��ȡֵ�أ����m��n��ֵ��ԭʽȥ���źϲ��������ֵ���м��㼴���������ʽ��ֵ. ���������(4x2��mx��3y��4)��(8nx2��x��2y��3) ��4x2��mx��3y��4��8nx2��x��2y��3 ��(4��8n)x2��(1��m)x��5y��7�� ����ʽ��ֵ����ĸx��ȡֵ�أ� ��4��8n��0��1��m��0����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��3�� ��ʽ����Ӽ� ��Ԫ���Ծ� ���ͣ���ѡ��
��m��n=��1����m��n��2��2m+2n��ֵ�ǣ�������
A. 3 B. 2 C. 1 D. ��1
A �������������������Ϊm��n = ��1�����ԣ�m��n��2��2m+2n=��m��n��2��2��m-n��=1+2=3����ѡ��A.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ɽ��ʡ��������У���꼶���ϣ���һ��������ѧ�Ծ� ���ͣ������
��������a��b���涨һ�����������������a��b=ab+a+b����x��3=4�Ľ���x=______��
0.25�� ����������a��b=ab+a+b�� ��̣�x��3=4�ɻ�Ϊ�� ����ã� . �ʴ�Ϊ�� .�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com