
 如图,在△ABC中,D为AB的中点,CE=3BE,CF=2AF,四边形CEDF的面积为17,则△ABC的面积为( )
如图,在△ABC中,D为AB的中点,CE=3BE,CF=2AF,四边形CEDF的面积为17,则△ABC的面积为( )| A. | 22 | B. | 23 | C. | 24 | D. | 25 |
分析 本题需先分别求出S△BED=$\frac{1}{3}$S△CED,S△AFD=$\frac{1}{2}$S△CDF,S△ACD=S△BCD,再根据S△CDE+S△CDF=17,列出方程组,解方程组即可求出结果.
解答  解:连接CD,
解:连接CD,
∵四边形CEDF的面积为17,设S△CED=x,S△CFD=y,
∴x+y=17,
∴CE=3BE,CF=2AF,
∴S△BED=$\frac{1}{3}$S△CED=$\frac{1}{3}$x,S△AFD=$\frac{1}{2}$S△CDF=$\frac{1}{2}$y,
∵D为AB的中点,
∴S△ACD=S△BCD,
∴x+$\frac{1}{3}$x=y+$\frac{1}{2}$y,
∴$\left\{\begin{array}{l}{x+y=17}\\{\frac{4}{3}x=\frac{3}{2}y}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=9}\\{y=8}\end{array}\right.$,
∴S△ABC=S△ACD+S△BCD=$\frac{4}{3}$×9+$\frac{3}{2}$×8=24.
故选C.
点评 本题考查三角形的面积,关键知道当高相等时,面积等于底边的比,根据此可求出三角形的面积,然后求出三角形面积的和.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,已知线段a;请你按下列步骤画图:(用圆规、三角板、量角器等工具画图,不写画法,只保留画图痕迹)
如图,已知线段a;请你按下列步骤画图:(用圆规、三角板、量角器等工具画图,不写画法,只保留画图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
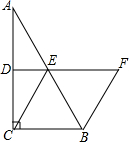 如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
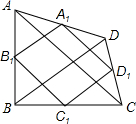 如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为9cm.
如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为9cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )| A. | y=6-$\frac{1}{2}$x(0<x<12) | B. | y=-$\frac{1}{2}$x2+6x(0<x<12) | ||
| C. | y=2x2-12x(0<x<12) | D. | y=$\frac{1}{2}$x2+6x(0<x<12) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com