
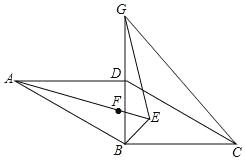
【题目】如图,在ABCD中,BD⊥BC,∠BDC=60°,∠DAB和∠DBC的平分线相交于点E,F为AE上一点,EF=EB,G为BD延长线上一点,BG=AB,连接GE.
(1)若ABCD的面积为9![]() ,求AB的长;
,求AB的长;
(2)求证:AF=GE.
【答案】(1)6;(2)证明见解析.
【解析】
(1)由平行四边形的性质得到AD与BC平行,利用等边三角形的判定可知三角形
ABG为等边三角形,得到三边相等,三角相等且为60°,再由BD垂直于BC,得到两个内
错角都为90°,进而求出∠DAB=30°,在直角三角形ADB中,利用30°所对的直角边等于斜
边的一半表示出BD,进而表示出AD,表示出平行四边形的面积,将表示出的AD,BD,
以及已知面积代入求出AB的长;
(2)连接BF,由AE,BE平分∠BAD、∠DBC,求出∠BAE与∠DBE的度数,利用内角
和定理求出∠AEB=60°,由EF=BE,得到三角形BFE为等边三角形,得到BE=BF,∠FBE=60°,
得到夹角相等,利用SAS得到三角形ABF与三角形GBE全等,利用全等三角形对应边相
等得到AF=GE即可得证.
(1)解:∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,
∵∠BDC=60°,
∴∠ABG=60°,
∵BG=AB,
∴△ABG为等边三角形,
∴AB=AG=BG,∠ABG=∠GAB=∠AGB=60°,
∵BD⊥BC,
∴∠ADB=∠DBC=90°,
∴∠DAB=![]() ∠GAB=30°,
∠GAB=30°,
在Rt△ADB中,![]()
∵S平行四边形ABCD=ADBD![]()
∴AB=6,即AG=6;
(2)证明:连接BF,
∵AE、BE分别平分∠BAD、∠DBC,
∴∠BAE=![]() ∠BAD=15°,∠DBE=
∠BAD=15°,∠DBE=![]() ∠DBC=45°,
∠DBC=45°,
∴∠ABE+∠BAE+∠AEB=180°,
∴∠AEB=60°,
∵EF=BE,
∴△BFE为等边三角形,
∴BE=BF,∠FBE=60°,
∴∠ABD=∠FBE=60°,
∴∠ABF=∠GBE,
在△ABF和△GBE中,
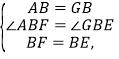
∴△ABF≌△GBE(SAS),
∴AF=GE.


科目:初中数学 来源: 题型:
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形外,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B逆时针旋转,使ON边与BC边重合,完成第一次旋转;再绕点C逆时针旋转,使MN边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B,O间的距离不可能是( )
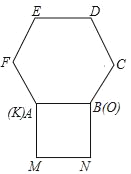
A. 0 B. 0.8 C. 2.5 D. 3.4
查看答案和解析>>
科目:初中数学 来源: 题型:
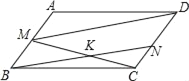
【题目】在ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
(1)求tan∠CMD的值;
(2)设N为CD中点,CM交BN于K,求![]() 及S△BKC的值.
及S△BKC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造,根据市政建设的需要,需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作,只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=32°,则∠ACF的度数为__________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
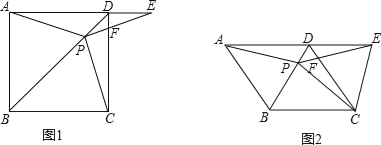
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫配方法.配方法的基本形式是完全平方公式的逆写,即![]() .请根据阅读材料解决下列问题:
.请根据阅读材料解决下列问题:
(1)填空:分解因式![]() _____;
_____;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 、
、![]() 、
、![]() 分别是
分别是![]() 的三边,且
的三边,且![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDF;
(2)若AB=4,BC=8,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com