
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),且过点
与x轴交于A,B两点(点A在点B的左侧),且过点![]() .
.
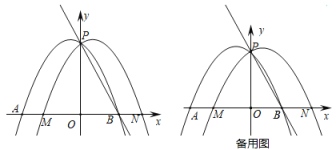
(1)直接写出a的值和点B的坐标;
(2)将抛物线向右平移2个单位长度,所得的新抛物线与x轴交于M,N两点,两抛物线交于点P,求点M到直线PB的距离;
(3)在(2)的条件下,若点D为直线BP上的一个动点,是否存在点D,使得![]() ?若存在,请求出点D的坐标:若不存在,请说明理由.
?若存在,请求出点D的坐标:若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)D点坐标为
;(3)D点坐标为![]() 或
或![]() .
.
【解析】
(1)将点(-2,4)代入y=a(x+5)(x3)即可求出a,根据抛物线解析式可直接得出点B的坐标;
(2)作![]() 于点C,连接MP,首先求出平移后的新抛物线解析式,得到点M、P的坐标,然后求出BP,利用S△PMB=
于点C,连接MP,首先求出平移后的新抛物线解析式,得到点M、P的坐标,然后求出BP,利用S△PMB=![]() ×PB×MC=
×PB×MC=![]() ×MB×OP,即可求解;
×MB×OP,即可求解;
(3)作BE平分![]() 交OP于E,作
交OP于E,作![]() 于F,根据
于F,根据![]() 求出
求出![]() ,然后在
,然后在![]() 中,可得
中,可得![]() ,然后分情况讨论:①点D在x轴上方,设AD交y轴于点H,根据
,然后分情况讨论:①点D在x轴上方,设AD交y轴于点H,根据![]() 求出点H的坐标,然后求得直线PB与直线AH的解析式,联立即可求出点D的坐标,②点D在x轴下方,设AD交y轴于点K,同理可求点D的另一个坐标.
求出点H的坐标,然后求得直线PB与直线AH的解析式,联立即可求出点D的坐标,②点D在x轴下方,设AD交y轴于点K,同理可求点D的另一个坐标.
解:(1)将点![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∵抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),
与x轴交于A,B两点(点A在点B的左侧),
∴![]() ;
;
(2)作![]() 于点C,连接MP,
于点C,连接MP,
由题意得:将点![]() 向右平移2个单位得到点M为
向右平移2个单位得到点M为![]() ,
,
原抛物线解析式为![]() ,
,
则新抛物线解析式为![]() ,
,
联立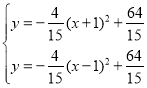 ,解得:
,解得:![]() ,
,
∴点P的坐标为![]() ,
,
∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵S△PMB=![]() ×PB×MC=
×PB×MC=![]() ×MB×OP,
×MB×OP,
∴![]() ,
,
即点M到直线PB的距离为![]() ;
;
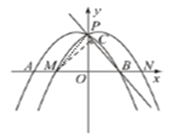
(3)存在符合题意的点D为![]() 或
或![]() ,
,
作BE平分![]() 交OP于E,作
交OP于E,作![]() 于F,
于F,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴在![]() 中,
中,![]() ,
,
分两种情况:
①如图,点D在x轴上方,设AD交y轴于点H,
∵![]() ,
,
∴![]() ,即
,即![]()
∴![]() ,
,
∴点H坐标为![]() ,
,
设直线PB的解析式为![]() ,
,
代入![]() 和
和![]() 得:
得:![]() ,解得:
,解得: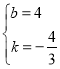 ,
,
∴直线PB的解析式为![]() ,
,
设直线AH的解析式为![]() ,
,
代入![]() 和
和![]() 得:
得: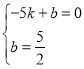 ,解得:
,解得:![]() ,
,
∴直线AH的解析式为![]() ,
,
联立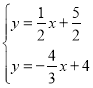 ,得
,得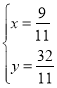 ,
,
∴直线AH与直线BP的交点坐标为![]() ;
;
②如图,点D在x轴下方,设AD交y轴于点K,
同①的方法可求得点D坐标为![]() ,
,
综上所述,存在满足题目条件的D点坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内, ![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() (2,-4),
(2,-4), ![]() (4,-4),
(4,-4), ![]() (1,-1).
(1,-1).

(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,直接写出点
,直接写出点![]() 的坐标;
的坐标;
(2)画出![]() 绕点
绕点![]() 逆时针旋转90°后的
逆时针旋转90°后的![]() ;
;
(3)在(2)的条件下,求线段![]() 扫过的面积(结果保留π).
扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+4x+5.
(1)用配方法将y=-x2+4x+5化成y=a(x﹣h)2+k的形式;
(2)指出抛物线的开口方向、对称轴和顶点坐标;
(3)若抛物线上有两点A(x1,y1),B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
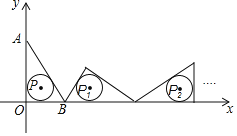
【题目】如图,把![]() 置于平面直角坐标系中,点A的坐标为
置于平面直角坐标系中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点P是
,点P是![]() 内切圆的圆心.将
内切圆的圆心.将![]() 沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为
沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为![]() ,第二次滚动后圆心为
,第二次滚动后圆心为![]() ,…,依此规律,第2019次滚动后,
,…,依此规律,第2019次滚动后,![]() 内切圆的圆心
内切圆的圆心![]() 的坐标是________.
的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线上的两个动点M、N,满足AB=![]() MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM取最小值时,线段AN的长度为( )
MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM取最小值时,线段AN的长度为( )
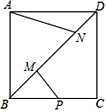
A.4B.2![]() C.6D.3
C.6D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
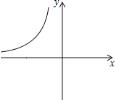
(1)图象的另一支在第________象限;在每个象限内,![]() 随
随![]() 的增大而________;
的增大而________;
(2)常数![]() 的取值范围是________;
的取值范围是________;
(3)若此反比例函数的图象经过点![]() ,求
,求![]() 的值.点
的值.点![]() 是否在这个函数图象上?点
是否在这个函数图象上?点![]() 呢?
呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文艺复兴时期,意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为![]() ,
,![]() 所在圆的圆心为点
所在圆的圆心为点![]() (或
(或![]() ). 若正方形的边长为2,则图中阴影部分的面积为( )
). 若正方形的边长为2,则图中阴影部分的面积为( )
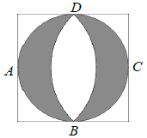
A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com